Description

如果我们定义 $f(0) = 1$，$f(1) = 0$，$f(4) = 1$，$f(8) = 2$，$f(16) = 1$ …… 你知道函数 $f$ 意味着什么吗？

其实，$f(x)$ 计算的是 $x$ 中每个数字所产生的封闭区域的总数。下表显示了每个数字产生的封闭区域数：

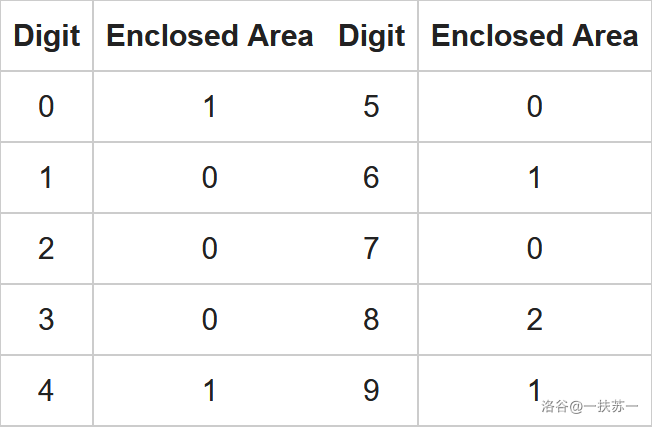
例如，$f(1234) = 0 + 0 + 0 + 1 = 1$，$f(5678) = 0 + 1 + 0 + 2 = 3$。

现在，我们用以下等式定义递归函数 $g$：

$$\begin{cases} g^0(x) = x \\ g^k(x) = f(g^{k-1}(x)) & \text{if } k \ge 1 \end{cases}$$

例如，$g^2(1234) = f(f(1234)) = f(1) = 0$，$g^2(5678) = f(f(5678)) = f(3) = 0$。

给定两个整数 $x$ 和 $k$，请计算 $g^k(x)$ 的值。

Input Format

有多个测试用例。输入的第一行包含一个整数 $T$（大约 $10 ^ 5$），表示测试用例的数量。 之后的每行包含两个整数 $x$ 和 $k$（$0 \le x, k \le 10^9$）。正整数不带前导零，零则正好是一个 "0"。

Output Format

对每个测试用例输出一行，其中包含一个整数，表示 $g^k(x)$ 的值。

6
123456789 1
888888888 1
888888888 2
888888888 999999999
98640 12345
1000000000 0

5
18
2
0
0
1000000000