Description

有一个著名的数学定理，如果你把一张公园的地图完全放在公园里，那么地图上存在一个点与它所代表的点重合。

Mio 非常喜欢这个定理，所以她把她最喜欢的公园的地图完全放在了公园里。公园 $P$ 可以用一个矩形表示。公园的地图只是一个较小（或相等）版本的公园在纸上的打印。地图与原始矩形相似。地图上的每个点都通过相似变换对应于公园中的一个点。

我们可以正式定义地图：地图是一个矩形 $M$（大小较小或相等），加上一个正实数 $r$ 和一个双射函数 $f:M \rightarrow P$，满足以下条件：

• 对于 $M$ 中的每对不同的点 $a, b$，$|f(a)-f(b)|/|a-b|=r$。

这里 $|x-y|$ 表示点 $x$ 和点 $y$ 之间的欧几里德距离。

就像许多游戏一样，Mio 可以使用地图进行传送。准确地说，当 Mio 在地图上的某个点 $x$（包括边界）时，她可以传送到公园中相应的点 $f(x)$。她也可以选择不传送。反之亦然。当她在公园中的点 $y$（包括边界）时，她可以传送到代表她当前位置的地图上的点 $f^{-1}(y)$。她也可以选择不传送。

Mio 最多可以传送 $n$ 次（最少为 $0$ 次）。每次传送需要 $k$ 秒。Mio 还可以以每秒 $1$ 个单位的速度步行。

给定两个点 $s$ 和 $t$，找出 Mio 从 $s$ 到 $t$ 需要的最短时间。

每次传送可以是任意方向（从地图到公园，或从公园到地图）。地图可以倒置放置。由于地图位于公园内部，所以 Mio 可能同时在地图上和在公园中。在这种情况下，她可以选择传送的方向。

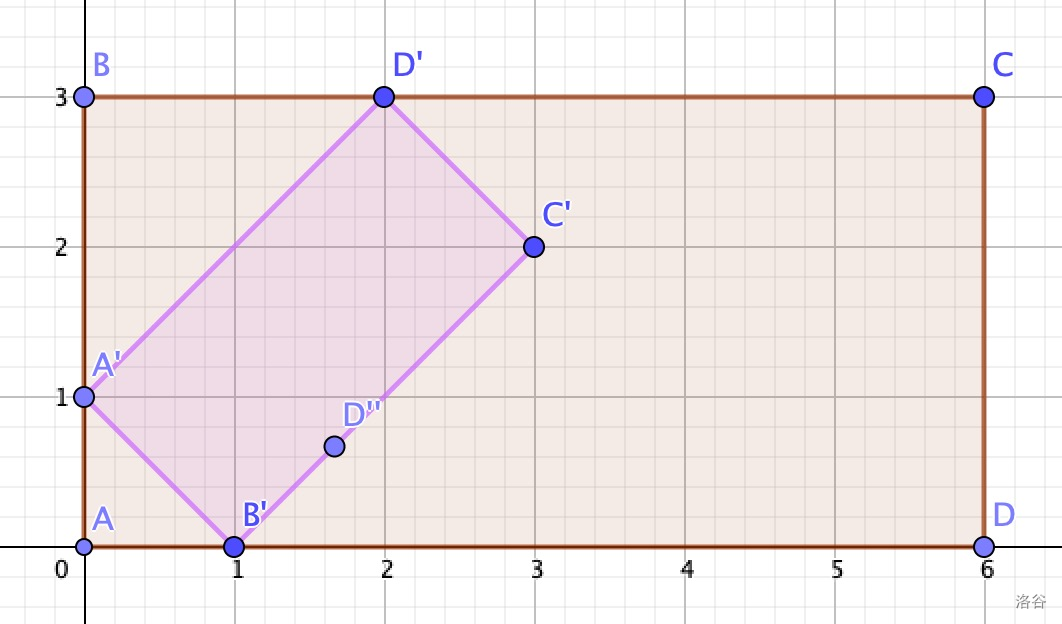
例如，在下图中，公园是 $ABCD$，地图是 $A'B'C'D'$。当 Mio 在地图上时，她同时在地图上和在公园中。当她在点 $D'$ 时，她可以从地图传送到公园（到达 $D$），并从公园传送到地图（到达 $D^{\prime\prime}$）。

Input Format

第一行包含一个整数 $T$（$1\le T\le 100$），表示测试用例的数量。

对于每个测试用例，第一行包含表示公园矩形的 $4$ 个角点。角点按顺时针或逆时针顺序给出。保证 $4$ 个角点不相同。

第二行包含表示地图矩形的 $4$ 个角点。地图的第 $i$ 个角点对应于公园的第 $i$ 个角点，对于所有 $1\le i\le 4$。请注意，您可以通过角点的顺序确定地图是否倒置放置。角点按顺时针或逆时针顺序给出。保证地图位于公园内部。（地图的边界可能与公园的边界在 $1$ 个或多个点相交。）保证地图是有效的，即存在一个正实数和一个从地图到公园的双射函数，满足上述的定义。

第三行包含两个点 $s$ 和 $t$。保证 $s$ 和 $t$ 在公园内部（或在公园的边界上）。

第四行包含两个整数 $k, n$（$0\le k\le 2\times 10^6, 0\le n\le 100$），表示每次传送所需的时间，以及最大传送次数。

输入中的每个点由一对整数表示，其绝对值不超过 $2\times 10^6$。整数之间用单个空格分隔。

Output Format

对于每个测试用例，输出一行数字表示答案。如果没有解决方案，则输出 $-1$。否则，输出最小的时间。您的答案被认为是正确的，如果其绝对或相对误差不超过 $10^{-9}$。

翻译来自于：ChatGPT。

2
0 0 0 2 4 2 4 0
0 0 0 1 2 1 2 0
2 1 4 2
1 1
0 0 0 3 6 3 6 0
0 1 1 0 3 2 2 3
0 0 4 2
0 3

1.0000000000
1.2272623352