Description

【题目背景】

都什么年代了还在做传统路径查询问题？

在阅读《Distributed Exact Shortest Paths in Sublinear Time》这篇论文后，您学会了如何在 $\mathcal{O}(D^{1/3} \cdot (n \log n)^{2/3})$ 的复杂度内解决分布式单源最短路问题。为了测试您是否真的学有所成，小青鱼为您准备了如下问题。

小青鱼有一张包含 $n$ 个节点与 $m$ 条无向边的图，节点编号从 $1$ 到 $n$。第 $i$ 条边连接节点 $u_i$ 和 $v_i$，边权为 $w_i$。

对于任意一条连接节点 $u$ 和 $v$ 的路径，定义路径的价值为路径上所有边的边权进行按位与（bitwise AND）计算的结果。

小青鱼很喜欢高价值的路径，因此他设定了一个固定的阈值 $V$。称小青鱼喜爱一条路径，当且仅当这条路径的价值至少为 $V$。

接下来，小青鱼将会提出 $q$ 次询问，第 $i$ 次询问可以用一对整数 $(u_i, v_i)$ 表示。对于每次询问，您需要判断节点 $u_i$ 到 $v_i$ 是否存在一条小青鱼喜爱的路径。

Input Format

每个测试文件仅有一组测试数据。

第一行输入四个整数 $n$，$m$，$q$ 和 $V$（$1 \le n \le 10^5$，$0 \le m \le 5 \times 10^5$，$1 \leq q \leq 5 \times 10^5$，$0 \leq V < 2^{60}$）表示图中的节点数以及边数，小青鱼的询问数以及固定阈值。

对于接下来 $m$ 行，第 $i$ 行输入三个整数 $u_i$，$v_i$ 和 $w_i$（$1 \le u_i,v_i \le n$，$u_i \ne v_i$，$0 \leq w_i < 2^{60}$）表示一条连接节点 $u_i$ 和 $v_i$ 的无向边，边权为 $w_i$。两个节点之间可能存在多条边。

对于接下来 $q$ 行，第 $i$ 行输入两个整数 $u_i$ 和 $v_i$（$1 \leq u_i, v_i \leq n$，$u_i \ne v_i$）表示一次询问。

Output Format

每次询问输出一行。若节点 $u_i$ 和 $v_i$ 之间存在一条价值至少为 $V$ 的路径输出 Yes，否则输出 No。

【样例解释】

接下来我们用 $\&$ 表示按位与计算。

第一组样例数据解释如下。

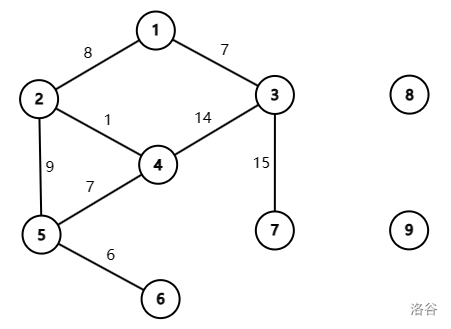
• 对于第一次询问，一条合法的路径为 $1 \to 3 \to 4 \to 5 \to 6$，其价值为 $7 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$。
• 对于第三次询问，一条合法的路径为 $7 \to 3 \to 4 \to 5 \to 6$，其价值为 $15 \,\&\, 14 \,\&\, 7 \,\&\, 6 = 6 \ge 5$。
• 对于第四次询问，因为节点 $1$ 与 $8$ 之间不存在任何路径，因此答案为 No。

对于第二组样例数据仅有的一次询问，可以考虑由第 $2$ 和第 $4$ 条边组成的路径，其价值为 $5 \,\&\, 6 = 4 \ge 4$。

9 8 4 5
1 2 8
1 3 7
2 4 1
3 4 14
2 5 9
4 5 7
5 6 6
3 7 15
1 6
2 7
7 6
1 8

Yes
No
Yes
No

3 4 1 4
1 2 3
1 2 5
2 3 2
2 3 6
1 3

Yes