#P9563. [SDCPC 2023] Be Careful 2
[SDCPC 2023] Be Careful 2
Description
小青鱼有一个位于二维平面上的,大小为 的矩形。矩形的右上角位于 ,而左下角位于 。矩形内部有 个禁止点,第 个禁止点位于 。
小青鱼想在矩形里画一个正方形。但由于小青鱼不喜欢禁止点,因此正方形的内部不能有任何禁止点。更正式地,小青鱼可以画一个左下角位于 且边长为 的正方形,当且仅当:
- 和 都是非负整数, 是一个正整数。
- 。
- 。
- 每个 都 不能 满足以下条件:
- 且 。
请计算小青鱼可以画的正方形的总面积。由于答案可能很大,请将答案对 取模后输出。
Input Format
每个测试文件仅有一组测试数据。
第一行输入三个整数 , 和 (,),表示矩形的大小和禁止点的数量。
对于接下来 行,第 行输入两个整数 和 (,)表示第 个禁止点的位置。保证所有禁止点互不相同。
Output Format
输出一行一个整数,代表对 取模后的答案。
【样例解释】
对于第一组样例数据,小青鱼有 种方式画一个正方形,如下图所示。
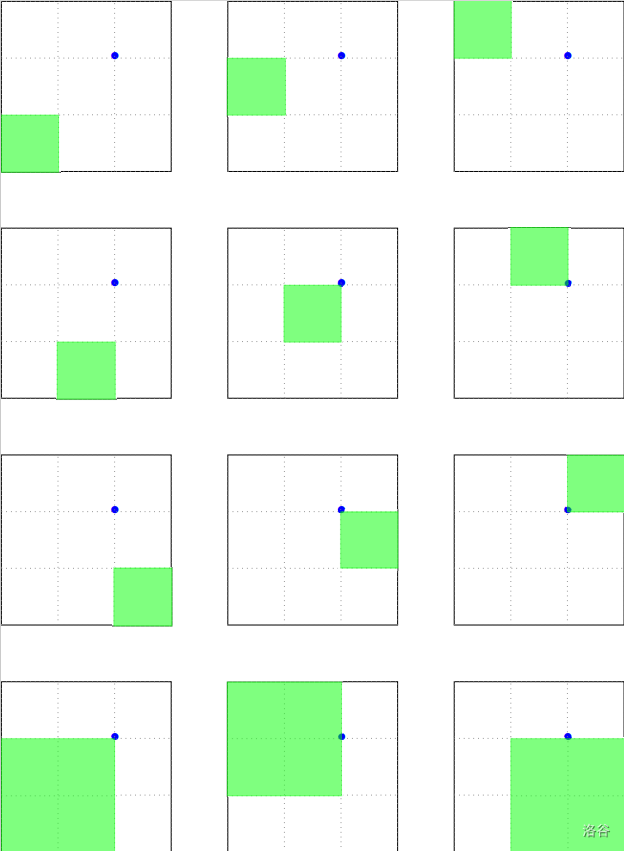
共有 个边长为 的正方形和 个边长为 的正方形。因此答案为 。
以下画正方形的方式是不合法的,因为正方形内有一个禁止点。
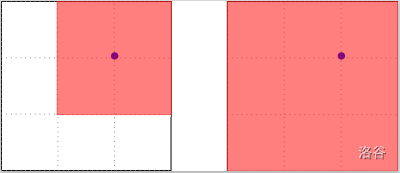
3 3 1
2 2
21
5 5 2
2 1
2 4
126

 京公网安备 11011102002149号
京公网安备 11011102002149号