Description

请回忆字典树的定义：

• 一棵大小为 $n$ 的字典树是一棵有 $n$ 个节点和 $(n - 1)$ 条边的有根树，每一条边都标有一个字符。
• 字典树中的每个节点都代表一个字符串，令 $s(x)$ 表示节点 $x$ 代表的字符串。
• 字典树的根代表的是空字符串。设节点 $u$ 为节点 $v$ 的父节点，设 $c$ 表示节点 $u$ 和 $v$ 之间的边上标有的字符，则 $s(v) = s(u) + c$。这里的 $+$ 代表字符串连接，而不是普通的加法。
• 所有节点代表的字符串互不相同。

给定一棵有 $(n + 1)$ 个节点的有根树，节点编号为 $0, 1, \cdots, n$，其中节点 $0$ 是根节点。树上共有 $m$ 个关键节点，其中第 $i$ 个关键节点的编号为 $k_i$。保证所有叶子节点都是关键节点。

请为每一条边标上一个小写字母，使得这棵有根树变为一棵大小为 $(n + 1)$ 的字典树。考虑所有关键节点代表的字符串构成的序列 $A = \{s(k_1), s(k_2), \cdots, s(k_m)\}$，设 $B = \{w_1, w_2, \cdots, w_m\}$ 是由序列 $A$ 中所有字符串按字典序从小到大排序后得到的字符串序列，您需要找到一个标记字母的方案，使得序列 $B$ 最小。

称长度为 $x$ 的字符串 $P = p_1p_2\cdots p_x$ 的字典序小于长度为 $y$ 的字符串 $Q = q_1q_2\cdots q_y$，若

• $x < y$ 且对于所有 $1 \le i \le x$ 有 $p_i = q_i$，或者
• 存在一个整数 $1 \le t \le \min(x, y)$，对于所有 $1 \le i < t$ 有 $p_i = q_i$，且 $p_t < q_t$。

称长度为 $m$ 的字符串序列 $F = \{f_1, f_2, \cdots, f_m\}$ 小于长度为 $m$ 的字符串序列 $G = \{g_1, g_2, \cdots, g_m\}$，若存在一个整数 $1 \le t \le m$，对于所有 $1 \le i < t$ 有 $f_i = g_i$，且 $f_t$ 的字典序小于 $g_t$ 的字典序。

Input Format

有多组测试数据。第一行输入一个整数 $T$ 表示测试数据组数。对于每组测试数据：

第一行输入两个正整数 $n$ 和 $m$（$1 \le m \le n \le 2 \times 10^5$）表示除了根节点以外的节点数量和关键节点的数量。

第二行输入 $n$ 个整数 $a_1, a_2, \cdots, a_n$（$0 \le a_i < i$），其中 $a_i$ 代表节点 $i$ 的父节点。保证每个节点至多有 $26$ 个子节点。

第三行输入 $m$ 个整数 $k_1, k_2, \cdots, k_m$（$1 \le k_i \le n$），其中 $k_i$ 代表第 $i$ 个关键节点的编号。保证所有叶子节点都是关键节点，且没有重复的关键节点。

保证所有测试数据 $n$ 之和不超过 $2 \times 10^5$。

Output Format

每组数据输出一行一个由小写字母组成的答案字符串 $c_1c_2\cdots c_n$，其中 $c_i$ 表示节点 $a_i$ 到 $i$ 的边上标有的小写字母。若有多种答案字符串使得字符串序列 $B$ 最小，请输出字典序最小的答案字符串。

【样例解释】

第一组样例数据的答案如下图所示。

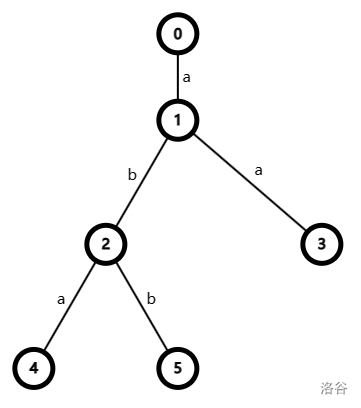
其中，节点 $1$ 代表的字符串为 a，节点 $4$ 代表的字符串为 aba，节点 $3$ 代表的字符串为 aa，节点 $5$ 代表的字符串为 abb。因此 $B = \{$a, aa, aba, abb$\}$。

2
5 4
0 1 1 2 2
1 4 3 5
1 1
0
1

abaab
a