#P9558. [SDCPC 2023] Trie
[SDCPC 2023] Trie
Description
Recall the definition of a trie:
- A trie of size is a rooted tree with vertices and edges, where each edge is marked with a character.
- Each vertex in a trie represents a string. Let be the string vertex represents.
- The root of the trie represents an empty string. Let vertex be the parent of vertex , and let be the character marked on the edge connecting vertex and , we have . Here indicates string concatenation, not the normal addition operation.
- The string each vertex represents is distinct.
We now present you a rooted tree with vertices. The vertices are numbered and vertex is the root. There are key vertices in the tree where vertex is the -th key vertex. It's guaranteed that all leaves are key vertices.
Please mark a lower-cased English letter on each edge so that the rooted tree changes into a trie of size . Let's consider the sequence consisting of all strings represented by the key vertices. Let be the string sequence formed by sorting all strings in sequence from smallest to largest in lexicographic order. Please find a way to mark the edges so that sequence is minimized.
We say a string of length is lexicographically smaller than a string of length , if
- and for all we have , or
- there exists an integer such that for all we have , and .
We say a string sequence of length is smaller than a string sequence of length , if there exists an integer such that for all we have , and is lexicographically smaller than .
Input Format
There are multiple test cases. The first line of th input contains an integer indicating the number of test cases. For each test case:
The first line contains two integers and () indicating the number of vertices other than the root and the number of key vertices.
The second line contains integers () where is the parent of vertex . It's guaranteed that each vertex has at most children.
The third line contains integers () where is the -th key vertex. It's guaranteed that all leaves are key vertices, and all key vertices are distinct.
It's guaranteed that the sum of of all test cases will not exceed .
Output Format
For each test case output one line containing one answer string consisting of lower-cased English letters, where is the letter marked on the edge between and . If there are multiple answers strings so that sequence is minimized, output the answer string with the smallest lexicographic order.
2
5 4
0 1 1 2 2
1 4 3 5
1 1
0
1
abaab
a
Hint
The answer of the first sample test case is shown as follows.
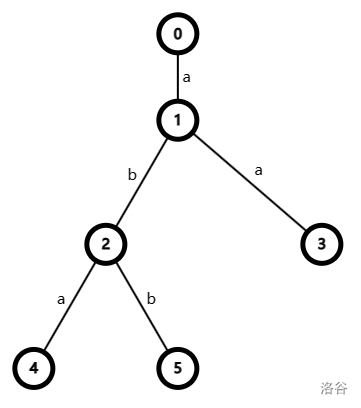
The string represented by vertex is a. The string represented by vertex is aba. The string represented by vertex is aa. The string represented by vertex is abb. So a, aa, aba, abb.

 京公网安备 11011102002149号
京公网安备 11011102002149号