Description

在游戏「石头、剪子、布」中，两名玩家分别同时出示自己的行动：石头、剪子、或布。如果两人的行动一致，则平局。否则石头打败剪子、布打败石头、剪子打败布。

上述过程可以重复多次。在本题中，两台有限状态自动机（Finite State Machines，FSM）将游玩多轮「石头、剪子、布」（准确地说，本题中的 FSM 特指 Moore 状态机）。

一台被设计用来游玩「石头、剪子、布」的 FSM 有着有限的状态。每个状态由以下信息描述：下一轮中本台自动机将会出示怎样的行动，以及当下一轮中对手出示了石头、剪子、或布时应该转移到的新状态。

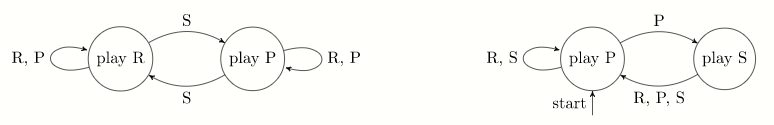
幸运的是，你知道对手的 FSM：你知道它所有的结构，但唯独不知道它的初始状态。

你的任务是设计一台你自己的 FSM 去和对手的进行对战。你的 FSM 必须在前十亿（${10}^9$）轮中打败对手至少 $99 \%$ 轮。这就是所谓的史诗般的胜利（epic win）！

对手的 FSM 持续出示石头或布（取决于初始状态）直到它接收到剪子：接收到剪子将导致它的行为改变。

一种打败这样的 FSM 的方法是出示布。如果对手持续出示石头，只需继续出示布即可胜利。如果对手出示了布，通过出示一次剪子让它的行为改变，接下来它就会持续出示石头，然后你就可以用布打败它了。

Input Format

从标准输入中读入对对手的 FSM 的描述，按如下格式：

第一行一个正整数 $n$，表示 FSM 中的状态数。所有状态从 $1$ 到 $n$ 编号。

接下来 $n$ 行，每行描述一个状态：一个字符 $c_i$ 以及三个正整数 $r_i, p_i, s_i$，分别表示该状态的行动、以及当对手出示了石头、布、或剪子后应该转移到的新状态的编号，其中 $c_i$ 只可能为 $\{\texttt{R}, \texttt{P}, \texttt{S}\}$ 之一，如果为 $\texttt{R}$ 则意味着行动为出示石头，如果为 $\texttt{P}$ 则意味着行动为出示布，如果为 $\texttt{S}$ 行动为出示剪子。

Output Format

将你设计的 FSM 以相同格式输出到标准输出中。

你的 FSM 的初始状态是 $1$ 号状态。

你的 FSM 的状态数量不应超过 $50000$。

【样例解释】

2
R 1 1 2
P 2 2 1

2
P 1 2 1
S 1 1 1

Hint

对于全部数据，$1 \le n \le 100$，$c_i \in \{\texttt{R}, \texttt{P}, \texttt{S}\}$，$1 \le r_i, p_i, s_i \le n$。

翻译来源：IOI 2021 集训队第一部分作业，PinkRabbit。