Description

让我们考虑以下构建图的方法。选择颜色数 $\hat{c}$。设 $n$ 为图中的顶点数。为了构建一个图，我们使用一个包含多个图的工作空间。每个图的每个顶点都有一个颜色。颜色由从 $1$ 到 $\hat{c}$ 的整数表示。最初，我们在工作空间中有 $n$ 个图，每个图中有一个顶点，所有顶点都被涂成颜色 $1$，且没有边。第 $i$ 个图的唯一顶点编号为 $i$。

允许以下操作：

join a $b$：将包含顶点 $a$ 和 $b$ 的图合并为一个图。不添加边。顶点 $a$ 和 $b$ 必须在不同的图中。

recolor a $c_{1}c_{2}$：在包含顶点 $a$ 的图中，将所有颜色为 $c_{1}$ 的顶点重新着色为颜色 $c_{2}$。

connect a $c_{1}c_{2}$：在包含顶点 $a$ 的图中，创建所有颜色为 $c_{1}$ 的顶点与颜色为 $c_{2}$ 的顶点之间的边。如果 $c_{1} = c_{2}$，则不创建自环。如果这样的边已经存在，则创建第二条平行边。在这个问题中不允许多重边，所以这种情况不应发生。

最后，我们应该有一个单一的图，并且其顶点的颜色无关紧要。

可以用来构建图的最小颜色数 $\hat{c}$ 称为图的团宽。团宽是图复杂度的特征之一。许多 NP 难问题可以在团宽有界的图上通过动态规划在这个构建图的过程中以多项式时间解决。对于一般图，计算团宽的确切值已知是 NP 难的。然而，对于某些图类，已知团宽的界限。

仙人掌图是一个连通的无向图，其中每条边最多位于一个简单环上。直观上，仙人掌图是树的推广，其中允许一些环。仙人掌图中不允许多重边（在一对顶点之间的多条边）和自环（连接顶点自身的边）。已知仙人掌图的团宽不超过 $4$。

给定一个仙人掌图。找出如何用最多 $\hat{c} = 4$ 种颜色以描述的方式构建它。

Input Format

输入文件的第一行包含两个整数 $n$ 和 $m (1 \le n \le 50 000$；$0 \le m \le 50 000)$。这里 $n$ 是图中的顶点数。顶点从 $1$ 到 $n$ 编号。图的边由一组边不同的路径表示，其中 $m$ 是这样的路径数。

接下来的 $m$ 行中的每一行包含图中的一条路径。路径以一个整数 $k_{i} (2 \le k_{i} \le 1000)$ 开头，后跟 $k_{i}$ 个从 $1$ 到 $n$ 的整数。这些 $k_{i}$ 个整数表示路径的顶点。路径中的相邻顶点是不同的。路径可以多次经过同一个顶点，但整个输入文件中每条边仅被遍历一次。

输入文件中的图是一个仙人掌图。

Output Format

在第一行打印一个整数 $q$——你需要的操作数。这个数字不应大于 $10^{6}$。在接下来的 $q$ 行中打印操作。每个操作由其首字母（j 表示 join，r 表示 recolor 和 c 表示 connect）及其参数按问题描述的顺序表示。

最后，在应用所有这些操作后，应该得到一个图，它等于输入中的仙人掌图。这意味着在输入图中连接的每对顶点之间应该正好有一条边，而在输入图中未连接的顶点之间不应有边。

8 2
5 1 2 3 4 7
5 4 5 6 1 8

17
r 2 1 2
j 2 3
c 2 1 2
r 6 1 2
j 5 6
c 6 1 2
r 4 1 3
j 4 3
j 4 6
j 4 7
c 4 3 1
r 4 3 1
r 8 1 2
r 1 1 3
j 1 8
j 1 4
c 1 3 2

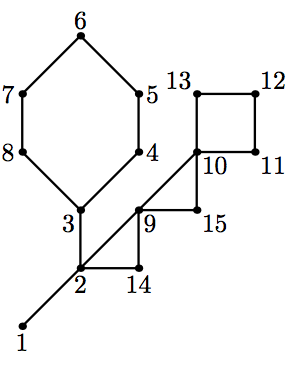
15 3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10

39
r 7 1 2
r 5 1 2
j 7 8
c 7 1 2
j 5 4
c 5 1 2
r 6 1 3
j 6 7
j 6 5
c 6 3 2
r 3 1 4
j 6 3
c 6 4 1
r 11 1 2
r 13 1 2
j 12 11
j 12 13
c 11 1 2
r 10 1 3
j 12 10
c 10 2 3
r 10 1 2
r 10 4 2
r 15 1 3
j 15 10
c 15 3 3
j 9 10
c 9 1 3
r 9 3 2
r 9 1 4
r 14 1 4
j 9 14
c 9 4 4
r 1 1 4
r 3 1 2
j 2 1
j 2 14
j 2 3
c 2 1 4

Hint

时间限制：2 秒，内存限制：512 MB。

题面翻译由 ChatGPT-4o 提供。