Description

原题面链接

qanat 是一种广泛用在气候炎热、干旱的地区中供水的灌溉系统。这项技术最初由波斯人在 $2000$ 多年前发明。在摩洛哥，qanat 被称为 khettara。至今该系统在该国南部地区仍然被使用。

qanat 的基本特点是用一个基本上是水平的沟渠，把水从地下水源带到靠近城市的出水口。还有一个被称为母井的轴垂直向上延升，从地下水源上升到山脉或山丘的地表。建设这样的系统非常昂贵，在古代更加如此，因为从沟渠和母井中挖出的所有材料都必须在地表运输。这可以通过沟渠出口或母井顶部来进行。为了帮助施工，通常在地下沟渠上方的关键位置还会放置一个或多个额外的垂直井口。尽管这些井口也必须需要被挖掘，但它们提供了一种从水平沟渠中运输额外泥土的手段，如图 $1$ 所示。

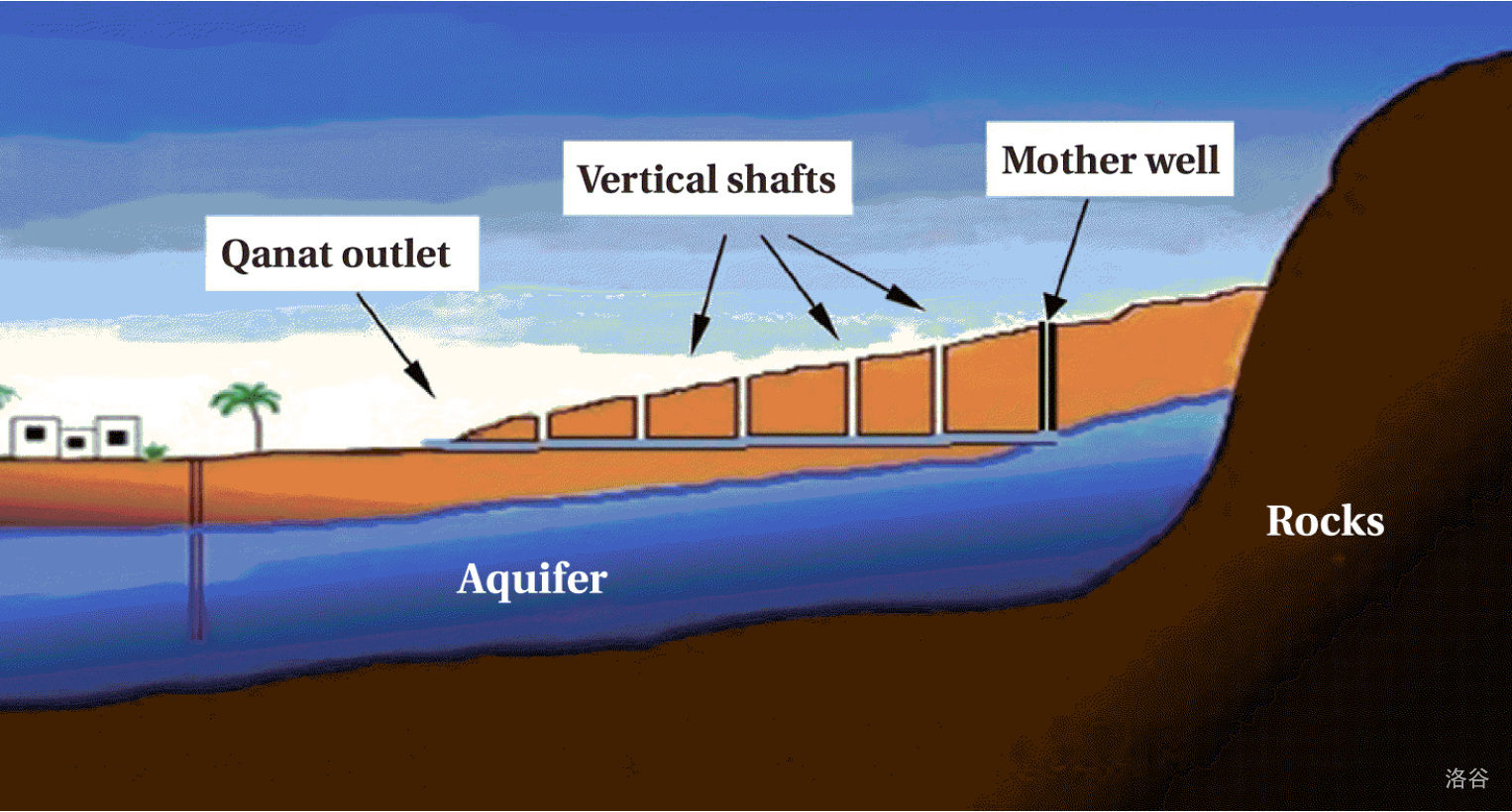
对于这个问题，模拟一个 qanat 的横截面，如图 $2$ 所示，其中通道出口在 $(0,0)$，水源在 $(w,0)$，母井顶部在 $(w,h)$，其中 $w > h$。山的表面沿着一条直线延伸，从 $(w,h)$ 到 $(0,0)$。

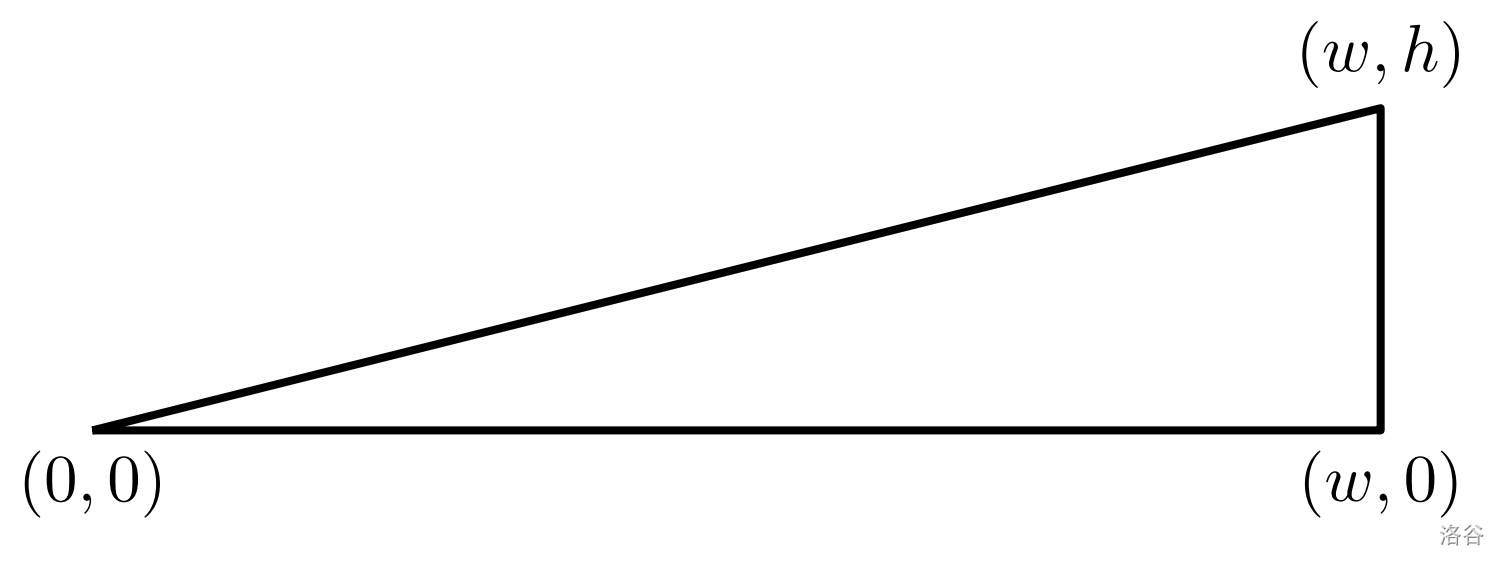
每个 qanat 必须从水源到山体表面上有一个垂直的母井，还需要 $n$ 个额外的垂直井。水道和所有垂直井都被建模为线段。你的目标是确定这些额外井的位置，以最小化整体的挖掘成本。这个成本等于每块挖掘的土壤必须被运输到表面的距离的总和（任何水平和垂直运动的组合）。例如，从表面开始并沿着长度为 $l$ 的路径挖掘连续的土壤的成本为 $\int_0^l x \ \mathop{}\!\mathrm{dx}=\frac{1}{2}l^2$。

Input Format

输入是一行，包含三个整数 $w$ $(1\le w\le 10000)$， $h$ $(1\le h<w)$，和 $n$ $(1\le n\le 1000)$，分别表示水源到 qanat 出口的水平距离，水源到山体表面的垂直距离和除了母井之外必须使用的垂直井口的数量。

Output Format

首先，输出最小开挖成本。接下来，按照递增顺序输出 $n$ 个最优放置的竖井的 $x$ 坐标。如果 $n > 10$，则仅输出前 $10$ 个 $x$ 坐标。相对误差可以在 $10^{-4}$ 之内。你可以假设存在唯一解决方案。没有数据会导致竖井距离 qanat 渠道出口或其他竖井小于0.001单位。

说明/提示

时间限制：$2000$ ms，空间限制：$1048576$ kB。

来源：

International Collegiate Programming Contest (ACM-ICPC) World Finals 2015

8 4 1

31.500000
3.000000

195 65 2

12220.000000
48.000000
108.000000

10000 1 1000

30141.885677
9.956721
19.913443
29.870164
39.826887
49.783610
59.740334
69.697060
79.653786
89.610515
99.567245