Description

在一个陌生的大城市中找到你的目的地可能是一个挑战，尤其是如果你像 Kirk 一样是一名计算机科学家，总是试图使用最短的路径。规划可以有所帮助——给定城市的地图，Kirk 想要找到他当前位置和目的地之间的最短路径。

城市的地图可以在平面上表示为由单位方格组成的无限网格。

Kirk 目前位于方格 (0, 0)，他的目的地是方格 (X, Y)。

城市中有 N 座建筑。每座建筑是一个完全占据若干单位方格的矩形。没有两座建筑接触或重叠，即 Kirk 可以自由地绕过每座建筑。建筑通过指定建筑占据的两个对角方格的坐标来定义。

在每一步中，Kirk 可以走到四个相邻方格之一，但他不能踏上被建筑占据的方格。他目前的位置在城市的西入口，每个被建筑占据的方格的 x 坐标严格大于零。

编写一个程序，给定建筑的位置，找到从 Kirk 当前的位置到他目的地的一条最短路径。路径应报告为一系列垂直和水平线段，且没有两个连续的线段是平行的。路径的长度是路径中包含的方格数，不包括初始方格。

Input Format

输入的第一行包含两个整数 X, Y (1 ≤ X ≤ 10^6, -10^6 ≤ Y ≤ 10^6)——目的地方格的坐标。输入的第二行包含一个整数 N (0 ≤ N ≤ 100,000)——城市中的建筑数量。接下来的 N 行中的每一行包含四个整数 X1, Y1, X2, Y2 (1 ≤ X1, X2 ≤ 10^6, -10^6 ≤ Y1, Y2 ≤ 10^6)——建筑占据的两个对角方格的坐标。

Output Format

输出的第一行应包含一个整数 L——到达目的地的最短路径的长度。输出的第二行应包含一个整数 M——最短路径中的线段数量。线段数量 M 不得超过 1,000,000。

接下来的 M 行中的每一行应包含两个整数 DX 和 DY，描述 Kirk 在一个线段中的相对移动。对于每个线段，恰好一个值 DX 或 DY 应为零，并且没有两个连续的线段是平行的。

注意：如果有多个解决方案，你应该输出其中任何一个。

9 1 
2 
5 -3 8 3 
10 -3 13 3

16

12 0 
5 
2 -1 3 1 
6 -7 8 -1 
6 1 8 6 
4 3 4 5 
10 -5 10 3

24

42 33
66
35 37 37 37
13 -41 13 6
40 -2 42 -1
27 -2 28 -2
15 -4 16 2
29 16 29 16
38 -34 38 -11
22 -5 22 -5
34 27 34 35
28 12 29 12
10 11 11 13
11 25 11 25
24 4 25 40
27 9 27 10
27 -4 27 -4
29 7 29 10
3 -13 5 -13
16 17 16 17
18 6 18 48
4 7 4 14
5 2 5 5
40 22 44 32
21 13 21 13
34 3 34 25
41 11 42 20
15 -15 16 -9
24 -46 25 -6
5 -4 5 -3
10 17 11 17
28 14 29 14
3 -15 4 -15
10 15 10 15
16 8 16 9
2 2 2 2
1 -4 3 -3
10 21 10 21
22 8 22 8
20 -3 21 2
10 19 11 19
7 -47 8 3
28 -11 28 -6
20 4 20 9
11 23 11 23
15 -17 16 -17
27 0 27 3
43 5 43 8
15 -7 16 -6
16 -19 16 -19
11 -10 11 -10
21 11 22 11
4 0 4 0
15 5 16 6
3 -11 5 -7
11 -8 11 -1
28 -13 28 -13
21 15 22 15
40 -30 43 -5
41 34 43 35
15 14 16 15
21 -16 22 -13
1 -1 2 -1
10 1 11 9
22 17 22 17
31 -50 32 -1
22 -8 22 -7
16 -21 16 -21

89

Hint

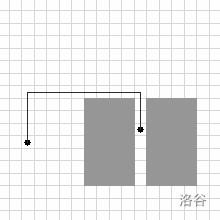
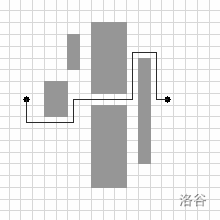
注意：原题还要求输出方案，本题略去。

题面翻译由 ChatGPT-4o 提供。