#P4671. [BalticOI 2011] Polygon (Day2)
[BalticOI 2011] Polygon (Day2)
Description
在一个无限的矩形网格上画了一个有 个顶点的简单多边形。对于这样的多边形,只有相邻的边在它们的公共顶点处相接;没有其他边相交或接触。多边形的所有顶点都位于网格点上,即顶点具有整数坐标。
你的任务是找到严格位于给定多边形内部的网格线段的总长度(这些线段在下面的图中被高亮显示)。
Input Format
输入的第一行包含一个整数 ,表示多边形的顶点数。接下来的 行中的每一行包含两个整数 和 ,表示一个顶点的坐标。顶点按顺时针或逆时针顺序给出。所有顶点都是不同的,但可能有多个连续的顶点位于一条线上。
Output Format
输出的唯一一行必须包含一个小数:严格位于给定多边形内部的网格线段的总长度。
3
5 1
2 4
1 1
10.0
5
0 0
-2 2
-2 -1
2 -2
2 0
12.5
Hint
样例解释 1
水平线的长度是 。垂直线的长度是 。总长度是 。
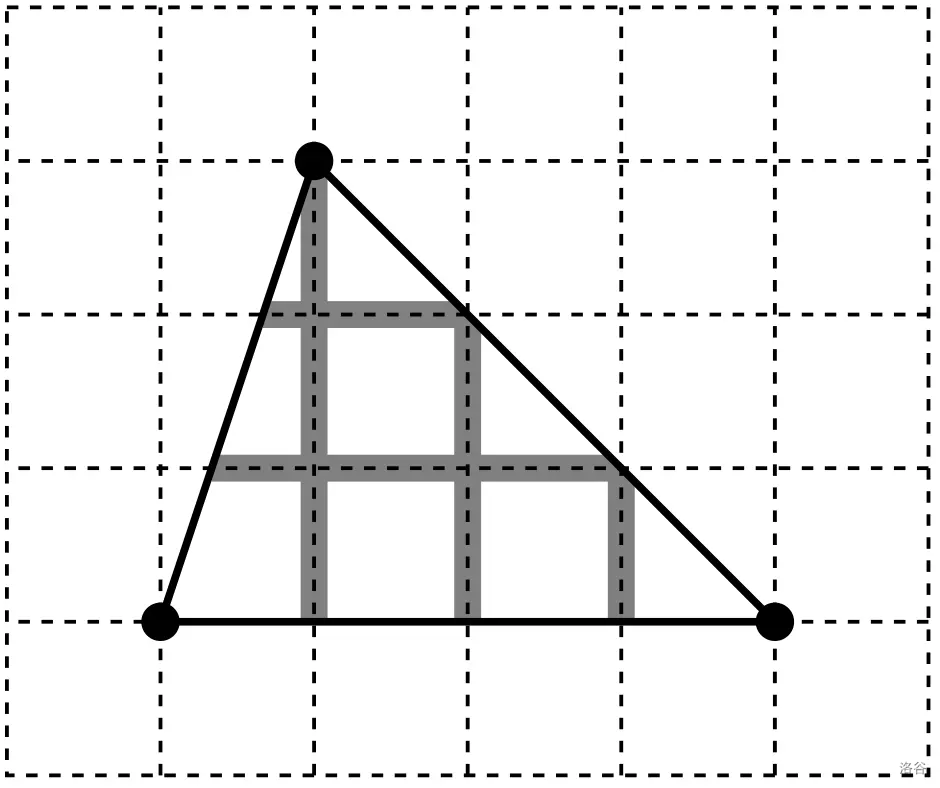
样例解释 2
水平线的长度是 。垂直线的长度是 。总长度是 。
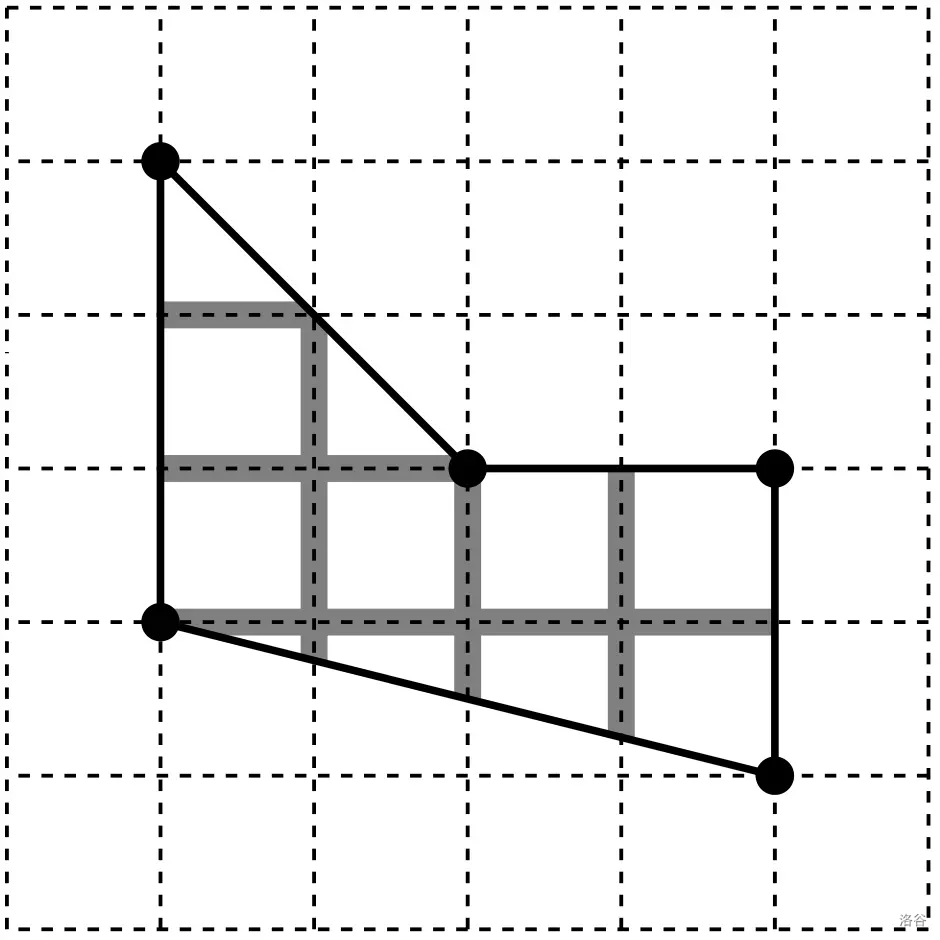
数据范围
对于 的数据,多边形的所有边均在网格线上。
对于所有数据,$3 \le N \le 10^5,-5 \times 10^8 \le x,y \le 5 \times 10^8$。
题面翻译由 ChatGPT-4o 提供。

 京公网安备 11011102002149号
京公网安备 11011102002149号