Description

盖盖乐是一人策略游戏。给定一个大棋盘，棋盘分成 $m\times n$ 个区块，相邻区块分别涂上白色与灰色以做区隔。每个区块都是个 $5\times 5$ 的方形小棋盘，每个小棋盘最多会有 $2$ 个特殊的格子。举例来说，下图是一个 $2\times 3$ 的大棋盘 $(m = 2, n = 3)$，其中有五个格子是特殊格子（以 $\texttt{X}$ 标示）。

:::align{center} :::

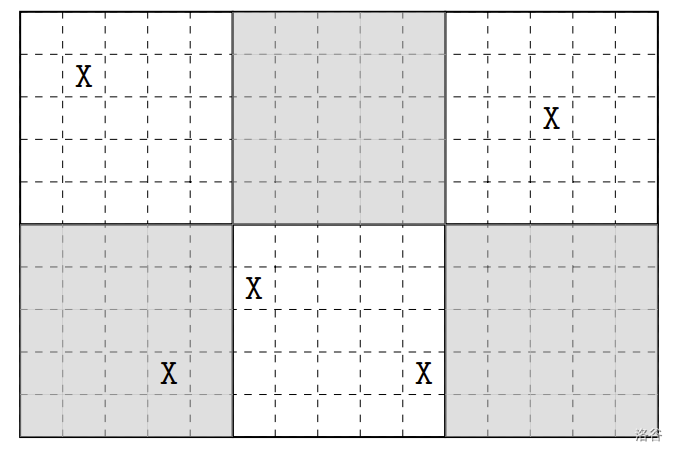盖盖乐有两种积木（如下图所示），分别可用以盖住棋盘上 $4$ 或 $3$ 个格子。两种积木分别可以任意旋转 $0, 90, 180, 270$ 度后再盖住棋盘格子，但是特殊的格子不可以被盖住。

:::align{center} :::

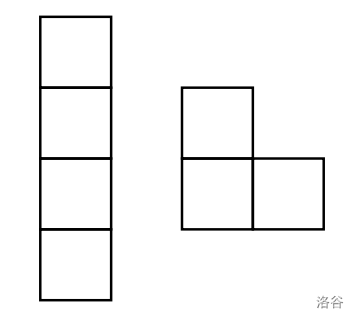请用以上两种积木把大棋盘盖满（特殊格子除外），使得共用积木的区块对越少越好。

• 也就是说，只要有两个区块共用了同一块积木，无论他们共用了几块，都会被算做一个「共用积木的区块对」。你的目标就是最小化这个区块对的数量。

在本題中，保证任意两个特殊格子皆不八方位相邻。也就是说，对于任两个特殊格子坐标 $(a, b), (c, d)$，皆有 $\max(|a - c|, |b - d|) > 1$。

Input Format

$$\begin{aligned} &n \ m \\ &a_{1, 1} \ a_{1, 2} \ \cdots \ a_{1, 5m} \\ &a_{2, 1} \ a_{2, 2} \ \cdots \ a_{2, 5m} \\ &\vdots \\ &a_{5n, 1} \ a_{5n, 2} \ \cdots \ a_{5n, 5m} \end{aligned}$$

• $n, m$ 为棋盘的大小。
• $a_{i, j}$ 代表棋盘第 $i$ 行第 $j$ 列的格子是否为特殊格子（也就是不能被盖住的格子），以 $0$ 或 $-1$ 表示，其中 $0$ 代表可被盖住的棋盘格子，$-1$ 代表特殊的格子。

Output Format

$$\begin{aligned} & b_{1, 1} \ b_{1, 2} \ \cdots \ b_{1, 5m} \\ & b_{2, 1} \ b_{2, 2} \ \cdots \ b_{2, 5m} \\ & \vdots \\ & b_{5n, 1} \ b_{5n, 2} \ \cdots \ b_{5n, 5m} \end{aligned}$$

请将棋盘盖满（特殊格子除外）后送回评分。积木盖住棋盘的表示方式如下:

• 同一块积木需以相同的正整数作为代号，例如 $1, 2, 3, \ldots$，但代号最大不可超过 $15000$。特殊格子必须维持以 $-1$ 代表之。
• 不同块积木不可以使用相同的代号。

Hint

示例

作为示例，假设测试资料的长相为

2 3
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 -1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 -1 0 0 0 0 0 -1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

则下面是一个可能的合法输出

1 1 2 2 3 3 11 12 12 12 12 21 21 21 21
1 -1 2 4 3 13 11 11 14 15 15 15 15 22 22
5 5 6 4 4 13 13 16 14 14 23 23 -1 22 24
5 7 6 6 8 8 17 16 16 18 23 25 25 24 24
9 7 7 10 8 19 17 17 20 18 18 25 26 27 27
9 9 28 10 10 19 19 35 20 20 41 26 26 27 42
29 29 28 28 30 -1 36 35 35 37 41 41 43 42 42
29 31 32 32 30 30 36 36 38 37 37 43 43 44 44
31 31 32 -1 33 33 39 38 38 -1 45 45 45 45 44
34 34 34 34 33 39 39 40 40 40 40 46 46 46 46

在这个示例中，最佳解的共用积木区块对数量为 $1$，而上面输出的任两个相邻区块都有共用积木，得到区块对数量为 $7$，表示 $p$ 和 $q$ 的值分别为 $1$ 和 $7$。因此，假设分数比重 $S=10$，这个输出可以获得 $S\cdot\max\left(\frac{1}{10}, \frac{1}{\sqrt{7 - 1 + 1}}\right) \approx 3.78$ 分。

可视化工具（Visualizer）

为了方便选手观看自己的输出结果以及观察测试资料，在此任务的附件（attachment）中，有一脚本程序（script）供选手可视化（visualize）输入档与输出档。

请利用下列指令可视化输入档。

python3 visualizer.py [input file]

你可利用下列指令，将你对于某个输入计算出的解做可视化。因为技术上的限制，附件中提供的可视化工具在棋盘过大时，仅会显示前 $10$ 排、以及前 $10$ 栏的方形小棋盘。

python3 visualizer.py [input file] --solution [output file]

为了方便辨识，程序会上色每块积木的方式输出，而不输出积木上面的数字。但由于颜色数量有限，程序会重新为所有积木上色并仅保证相邻的积木不同色。

示例：

python3 visualizer.py input_1_1.txt --solution output_1_1.txt

请注意，若你传入的资料的格式并不合法，将会产生一些不可预期的行为。不过，当你的解答唯一违反的规则是「未盖满所有格子」时，将未被盖到的格子留下数字 $0$ 会让该格子呈现白色，并正常的进行可视化。

一张使用前面示例所提到的可视化成果图如下：

:::align{center} :::

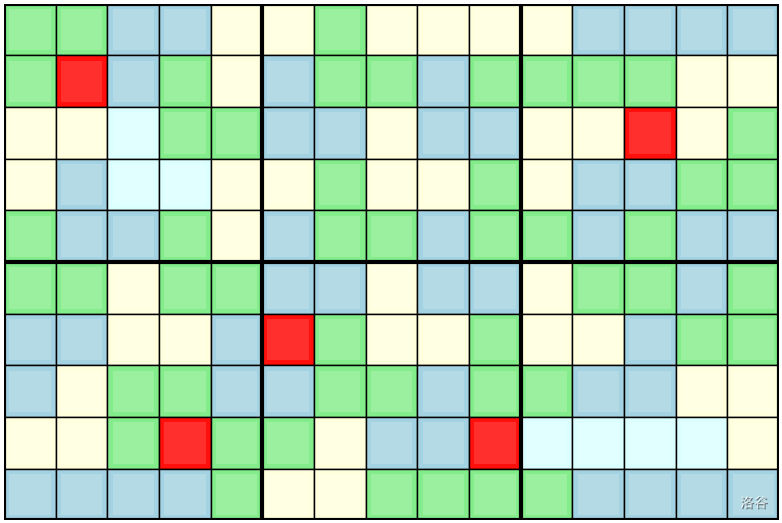数据限制

• $1\le n\times m\le 1600$。
• $-1 \leq a_{i, j} \leq 0$。
• 输入的数字皆为整数。
• 保证任一个被划分出来的 $5\times 5$ 方形小棋盘内，特殊格子数量都不超过 $2$。
• 保证存在一种可以盖满棋盘的方式。
• 保证任意两个特殊格子皆不八方位相邻。

评分说明

本题共有 10 组测试资料，输入档案的说明如表所示。 对于每一组测试资料，若你上传的输出档案满足输出格式，并且成功盖满了所有除了特殊格子以外的格子，那么你会得到以下分数

$$S \cdot \max\left(\frac{1}{10}, \frac{1}{\sqrt{q - p + 1}}\right)$$

其中 $S$ 是该测试资料的分数比重，$p$ 是最佳解的共用积木区块对数量、$q$ 是你给出的构造内的共用积木区块对数量。

若你上传的输出档案不满足输出格式、或是没有盖满所有除了特殊格子以外的格子，那么你将得到 $0$ 分。

测试资料	分数比重 $S$	输入档名	输出档名	说明
1	4	input_1_1.txt	output_1_1.txt	$n = 1$，$m = 1$。
2		input_2_1.txt	output_2_1.txt	$n = 1$，$m = 2$。
3	6	input_3_1.txt	output_3_1.txt	$n = 1$，$m = 3$。
4	8	input_4_1.txt	output_4_1.txt	$n = 2$，$m = 2$。
5	10	input_5_1.txt	output_5_1.txt	$n = 10$，$m = 10$。
6	12	input_6_1.txt	output_6_1.txt
7	8	input_7_1.txt	output_7_1.txt	$n = 1$，$m = 1599$。
8	20	input_8_1.txt	output_8_1.txt	$n = 20$，$m = 24$。
9		input_9_1.txt	output_9_1.txt	$n = 40$，$m = 40$。
10	8	input_10_1.txt	output_10_1.txt	$n = 39$，$m = 39$。