Description

给定一个连通图的平面嵌入。图中的每个顶点对应于一个具有整数坐标的不同点。两个顶点之间的每条边对应于连接这两个顶点对应点的直线段。由于给定的嵌入是平面的，对应边的线段除公共端点外不共享任何点。给定的嵌入被组织成使得所有线段的倾斜度都是 $45$ 度的倍数。换句话说，对于存在边的两个顶点 $u$ 和 $v$，其对应坐标分别为 $(x_u, y_u)$ 和 $(x_v, y_v)$，则满足 $x_u = x_v$、$y_u = y_v$ 或 $|x_u - x_v| = |y_u - y_v|$ 中的一个。

:::align{center}

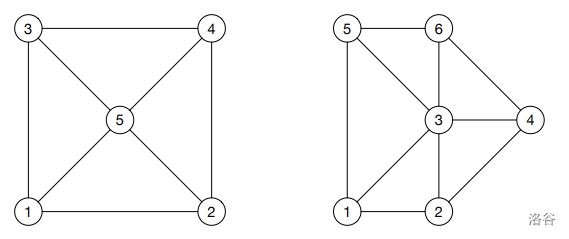
图 H.1. 样例输入 1 和 2 :::

你的任务是为每个顶点涂上四种颜色 $\{1, 2, 3, 4\}$ 中的一种，使得有边连接的两个顶点颜色不同。根据著名的四色定理，这样的着色总是可能的。请找出一种着色方案。

Input Format

输入包含单个测试用例，格式如下。

$$\begin{aligned} & n \; m \\ & x_1 \; y_1 \\ & \vdots \\ & x_n \; y_n \\ & u_1 \; v_1 \\ & \vdots \\ & u_m \; v_m \end{aligned}$$

第一行包含两个整数 $n$ 和 $m$。$n$ 是顶点数，$m$ 是边数，满足 $3 \leq n \leq m \leq 10\,000$。顶点编号为 $1$ 到 $n$。接下来的 $n$ 行中，每行包含两个整数。第 $v$ 行的整数 $x_v$ （$0 \leq x_v \leq 1000$）和 $y_v$ （$0 \leq y_v \leq 1000$）表示顶点 $v$ 对应点的坐标。顶点对应于不同的点，即对于 $u \neq v$，满足 $(x_u, y_u) \neq (x_v, y_v)$。接下来的 $m$ 行中，每行包含两个整数。第 $i$ 行的整数 $u_i$ 和 $v_i$，满足 $1 \leq u_i < v_i \leq n$，表示存在一条连接顶点 $u_i$ 和 $v_i$ 的边。

Output Format

输出应由 $n$ 行组成。输出的第 $v$ 行应包含一个整数 $c_v \in \{1, 2, 3, 4\}$，表示顶点 $v$ 将被涂色为 $c_v$。输出必须满足对于图中每条连接 $u$ 和 $v$ 的边，都有 $c_u \neq c_v$。如果有多个解，你可以输出其中任意一个。

5 8
0 0
2 0
0 2
2 2
1 1
1 2
1 3
1 5
2 4
2 5
3 4
3 5
4 5

1
2
2
1
3

6 10
0 0
1 0
1 1
2 1
0 2
1 2
1 2
1 3
1 5
2 3
2 4
3 4
3 5
3 6
4 6
5 6

1
2
3
4
2
1