Description

为了满足 ICPC（国际可可种植联盟）的需求，你必须检查两棵给定的树是否是双胞胎。

:::align{center}

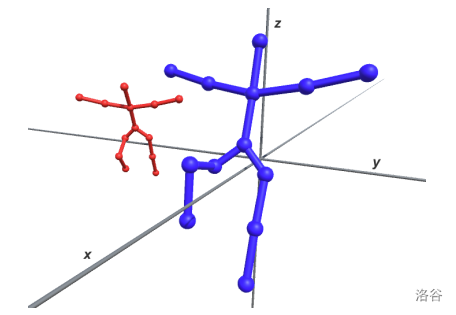
三维空间中两棵树的示例。 :::

图论中的术语树指的是一个连通图，其中边的数量比节点的数量少 $1$。此外，ICPC 将三维网格点作为树节点的位置。他们对于两棵树是双胞胎的定义是：存在一个几何变换函数，能将一棵树的所有节点一一映射到另一棵树的节点上，使得对于一棵树的每条边，另一棵树中都存在一条边连接相应的节点。该几何变换应为以下变换的组合：

• 平移：坐标值加上某些常数。
• 具有正比例系数的均匀缩放：所有三个坐标值乘以相同的正常数。
• 围绕 $x$ 轴、$y$ 轴和 $z$ 轴进行任意角度的旋转。

注意，两棵树可能以不止一种方式成为双胞胎，即具有不同的节点对应关系。

编写一个程序，判断两棵树是否是双胞胎，并输出不同节点对应关系的数量。

在下文中，变换将在右手 $xyz$ 坐标系中描述。

样例输入 $1$ 到 $4$ 中的树如下图所示。图中的数字是下面定义的节点编号。

:::align{center} :::

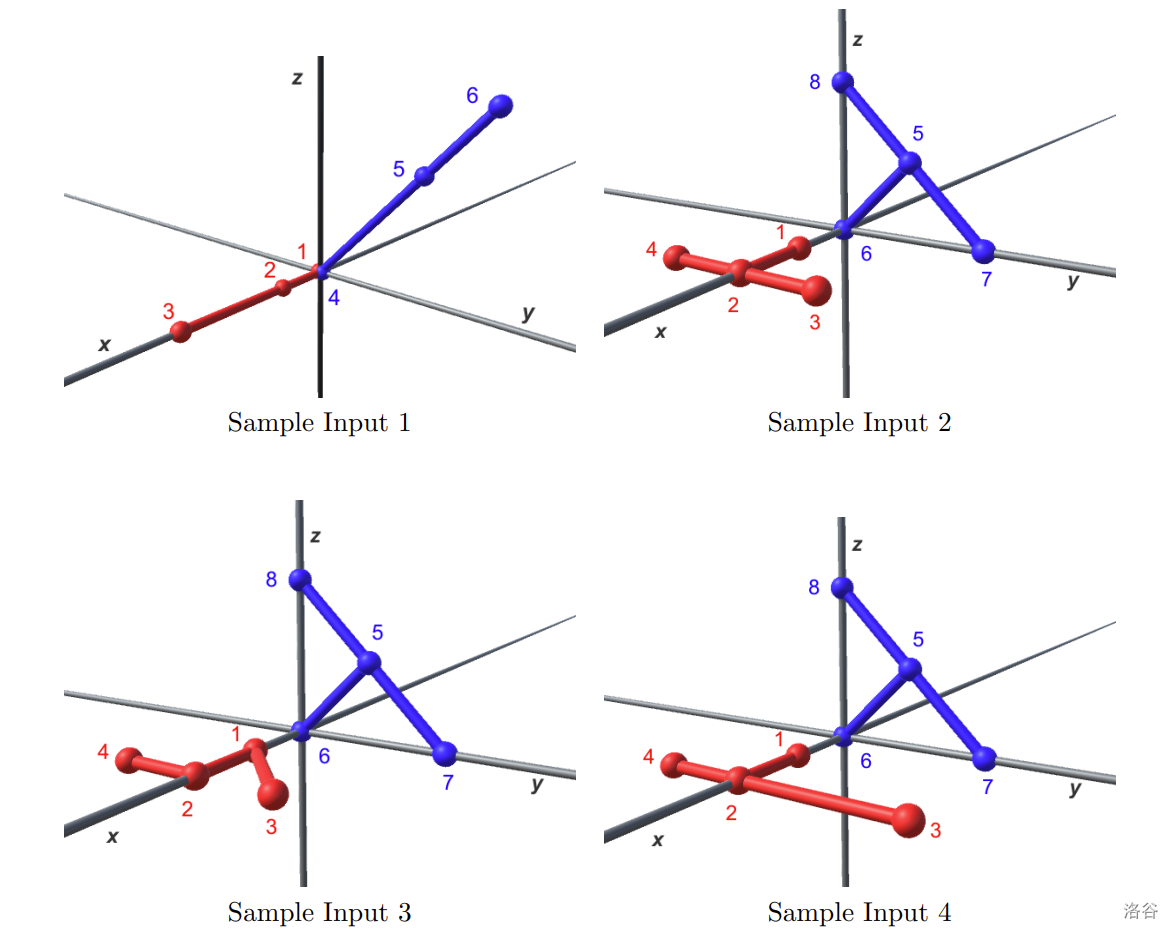对于样例输入 $1$，红色树的每个节点通过以下变换映射到蓝色树的对应节点：平移 $(-3,0,0)$，绕 $z$ 轴旋转 $-\pi/2$，绕 $x$ 轴旋转 $\pi/4$，最后缩放 $\sqrt{2}$ 倍。通过此映射，红色树中位于 $(0,0,0)$、$(1,0,0)$ 和 $(3,0,0)$ 的节点 $\#1$、$\#2$ 和 $\#3$ 分别对应蓝色树中位于 $(0,3,3)$、$(0,2,2)$ 和 $(0,0,0)$ 的节点 $\#6$、$\#5$ 和 $\#4$。这是这对双胞胎树唯一可能的对应关系。

对于样例输入 $2$，红色节点 $\#1$、$\#2$、$\#3$ 和 $\#4$ 可以映射到蓝色节点 $\#6$、$\#5$、$\#7$ 和 $\#8$。还存在另一种节点对应关系，将节点 $\#1$、$\#2$、$\#3$ 和 $\#4$ 映射到 $\#6$、$\#5$、$\#8$ 和 $\#7$。

对于样例输入 $3$，这两棵树不是双胞胎。存在将一棵树的节点映射到另一棵树不同节点的变换，但边的连接关系不匹配。

对于样例输入 $4$，不存在将一棵树的节点映射到另一棵树节点的变换。

Input Format

输入包含单个测试用例，格式如下。

$$\begin{aligned} &n \\ &x_1\ y_1\ z_1 \\ &\vdots \\ &x_n\ y_n\ z_n \\ &u_1\ v_1 \\ &\vdots \\ &u_{n-1}\ v_{n-1} \\ &x_{n+1}\ y_{n+1}\ z_{n+1} \\ &\vdots \\ &x_{2n}\ y_{2n}\ z_{2n} \\ &u_n\ v_n \\ &\vdots \\ &u_{2n-2}\ v_{2n-2} \end{aligned}$$

输入描述了两棵树。第一行包含一个整数 $n$，表示每棵树的节点数量（$3 \le n \le 200$）。接下来是两棵树的描述。

一棵树的描述由 $n$ 行给出顶点位置，以及 $n-1$ 行显示顶点的连接关系。

第一棵树的节点编号为 $1$ 到 $n$，第二棵树的节点编号为 $n+1$ 到 $2n$。

三元组 $(x_i, y_i, z_i)$ 给出了编号为 $i$ 的节点的坐标。$x_i$、$y_i$ 和 $z_i$ 是介于 $-1000$ 和 $1000$ 之间（含）的整数。单棵树的节点坐标互不相同。

整数对 $(u_j, v_j)$ 表示编号为 $u_j$ 和 $v_j$ 的节点之间存在一条边（$u_j \ne v_j$）。对于 $1 \le j \le n-1$，满足 $1 \le u_j \le n$ 和 $1 \le v_j \le n$；对于 $n \le j \le 2n-2$，满足 $n+1 \le u_j \le 2n$ 和 $n+1 \le v_j \le 2n$。

Output Format

如果两棵树是双胞胎，则输出不同节点对应关系的数量。否则，输出 $0$。

3
0 0 0
1 0 0
3 0 0
1 2
2 3
0 0 0
0 2 2
0 3 3
4 5
5 6

1

4
1 0 0
2 0 0
2 1 0
2 -1 0
1 2
2 3
2 4
0 1 1
0 0 0
0 2 0
0 0 2
5 6
5 7
5 8

2

4
1 0 0
2 0 0
2 1 0
2 -1 0
1 2
1 3
2 4
0 1 1
0 0 0
0 2 0
0 0 2
5 6
5 7
5 8

0

4
1 0 0
2 0 0
2 2 0
2 -1 0
1 2
2 3
2 4
0 1 1
0 0 0
0 2 0
0 0 2
5 6
5 7
5 8

0

3
0 0 0
0 0 1
0 0 2
1 2
1 3
10 4 6
0 0 0
5 2 3
4 5
5 6

1

4
0 0 0
1 3 3
-1 5 5
-10 2 2
1 2
1 3
1 4
1 1 6
0 0 0
-1 -1 10
-10 -10 4
5 6
6 7
6 8

1

7
0 0 0
1 0 0
-1 0 0
0 1 0
0 -1 0
0 0 1
0 0 -1
1 2
1 3
1 4
1 5
1 6
1 7
0 0 0
2 0 0
-2 0 0
0 2 0
0 -2 0
0 0 2
0 0 -2
8 9
8 10
8 11
8 12
8 13
8 14

24