Description

Boat 先生拥有大片土地。由于今年日本遭受了许多台风袭击，他开始担心自己地产的洪水风险，并想知道其土地的平均海拔。土地面积太大，无法在许多地点测量海拔。由于地产中没有陡坡，他认为只需要在有限数量的地点测量海拔，然后基于这些测量结果来估算其余地点的海拔就足够了。

基于相同的测量结果，可能存在多种估算方式。在这种情况下，他想知道最坏的情况，即给出最低平均海拔的情况。

Boat 先生的地产呈矩形，被划分为网格对齐、大小相同的矩形区域。其中一些区域已经进行了海拔测量，现在手头有测量结果。其余区域的海拔将基于以下假设进行估算：共享一条边的两个相邻区域的海拔差最多为 $1$。

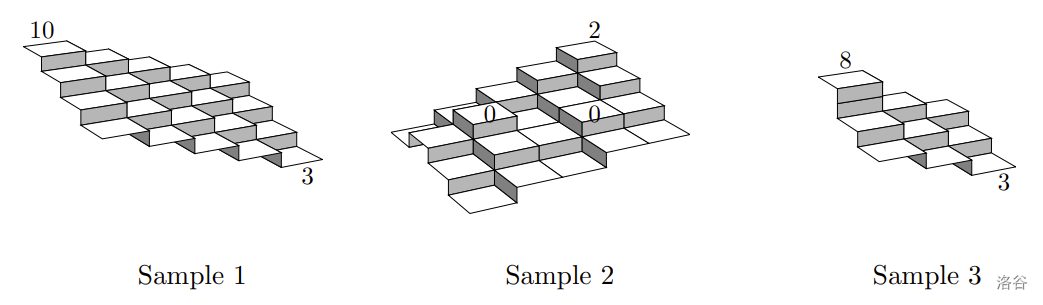
在下面给出的第一个样例中，土地被划分为 $5 \times 4$ 个区域。位置 $(1,1)$ 和 $(5,4)$ 的区域测量海拔分别为 $10$ 和 $3$。在这种情况下，假设相邻区域的海拔差最多为 $1$，所有区域的海拔被唯一确定。

在第二个样例中，存在多种可能性，应考虑其中给出最低平均海拔的那种。

在第三个样例中，没有海拔分配能满足关于海拔差的假设。

:::align{center} :::

你的任务是编写一个程序来估算他地产的平均海拔。准确地说，程序应计算所有网格划分区域的估算海拔和测量海拔的总和。如果存在两种或多种不同的估算方式，程序应计算最严苛的估算方式下的总和，即给出最低海拔总和的那种方式。

Input Format

输入包含单个测试用例，格式如下。

$$\begin{aligned} &w\ d\ n \\ &x_1\ y_1\ z_1 \\ &\vdots \\ &x_n\ y_n\ z_n \end{aligned}$$

其中，$w$、$d$ 和 $n$ 是介于 $1$ 到 $50$ 之间（含）的整数。$w$ 和 $d$ 是土地两个方向上的区域数量。$n$ 是进行了海拔测量的区域数量。接下来的 $n$ 行中，第 $i$ 行包含三个整数 $x_i$、$y_i$ 和 $z_i$，满足 $1 \le x_i \le w$，$1 \le y_i \le d$，且 $-100 \le z_i \le 100$。它们表示位于 $(x_i, y_i)$ 的区域的测量海拔为 $z_i$。同一区域最多给出一个测量结果，即对于 $i \ne j$，有 $(x_i, y_i) \ne (x_j, y_j)$。

Output Format

如果所有未测量的区域都能在不与测量海拔冲突的情况下分配海拔，且假设两个相邻区域的海拔差最多为 $1$，则输出一个整数，即所有区域的测量或估算海拔的总和。如果存在多种这样的海拔分配方式，则输出可能分配方式中的最小海拔总和。

如果没有海拔分配能满足海拔差假设，则输出 No。

5 4 2
1 1 10
5 4 3

130

5 4 3
2 2 0
4 3 0
5 1 2

-14

3 3 2
1 1 8
3 3 3

No

2 2 1
1 1 -100

-404