Description

Alice 和 Bob 正在使用一辆玩具太阳能车玩一个行李运送游戏。游戏场地中到处都放置了一些杆子。

在游戏开始时，太阳能车被放置在紧邻某个杆子的位置，并且同一个或另一个杆子被标记为目的地。Bob 选择其中一个杆子并将行李放在那里。然后，Alice 规划一条路线让小车去拾取行李并将其运送到标记的目的地。Alice 会选择最短的可能路线，而 Bob 应该选择一个杆子以使路线长度最大化。

太阳能车可以沿任意路线行驶，但由于它没有电池，一旦进入阴影就会停止。在这个游戏中，点光源位于场地的表面上，因此杆子会朝着与光源位置相反的方向投下无限长的阴影。行驶路线应避开所有这些阴影。

当给定太阳能车的初始位置和目的地位置时，假设两位玩家都做出最佳选择，行驶路线的长度是唯一确定的。

让我们考虑所有可能的游戏配置，给定两组杆子，一组用于太阳能车的起始位置，另一组用于目的地。当初始小车位置和目的地都从相应的集合中均匀随机选择时，期望的路线长度是多少？

你的任务是在给定小车的初始位置集合和目的地集合的情况下，计算路线长度的期望值。

Input Format

输入包含单个测试用例，格式如下。

$$\begin{aligned} &n \\ &x_1 \ y_1 \\ &\vdots \\ &x_n \ y_n \\ &p \\ &a_1 \ b_1 \ c_1 \ d_1 \\ &\vdots \\ &a_p \ b_p \ c_p \ d_p \end{aligned}$$

其中，$n$ 是杆子的数量（$3 \le n \le 2000$）。杆子编号为 $1$ 到 $n$，第 $i$ 个杆子放置在整数坐标 $(x_i, y_i)$ 处（$-1000 \le x_i \le 1000$，$-1000 \le y_i \le 1000$）。点光源位于 $(0,0)$。杆子不会放置在 $(0,0)$，也不会放置在另一个杆子的阴影中，且没有两个杆子放置在同一坐标。

$p$ 是集合对的数量（$1 \le p \le 10^5$）。第 $i$ 对集合由四个整数 $(a_i, b_i, c_i, d_i)$ 指定（$1 \le a_i \le b_i \le n$，$1 \le c_i \le d_i \le n$）。具体来说，太阳能车初始放置在第 $j$ 个杆子处，其中 $j$ 是从 $\{a_i, \dots, b_i\}$ 中均匀随机选择的，目的地杆子也是从 $\{c_i, \dots, d_i\}$ 中均匀随机选择的。

Output Format

为每一对集合输出答案。允许的绝对误差或相对误差小于 $10^{-7}$。

5
7 0
3 3
0 7
-3 3
-7 0
6
1 1 3 3
3 3 4 4
1 1 5 5
5 5 2 2
2 2 4 4
1 5 1 5

24.000000000000
20.440306508911
20.000000000000
19.000000000000
15.440306508911
21.606571644990

Hint

对于此测试用例的第一对集合，太阳能车放置在 $(7,0)$，旗帜放置在 $(0,7)$。然后，Bob 将行李放置在 $(-7,0)$。从 $(-7,0)$ 到 $(0,7)$ 的最短路线长度为 $10$，因为从 $(-7,0)$ 到 $(0,7)$ 的直线路径穿过了 $4$ 号杆子的阴影。从 $(7,0)$ 到 $(-7,0)$ 的最短路线长度为 $14$，因此总长度为 $24$。

:::align{center}

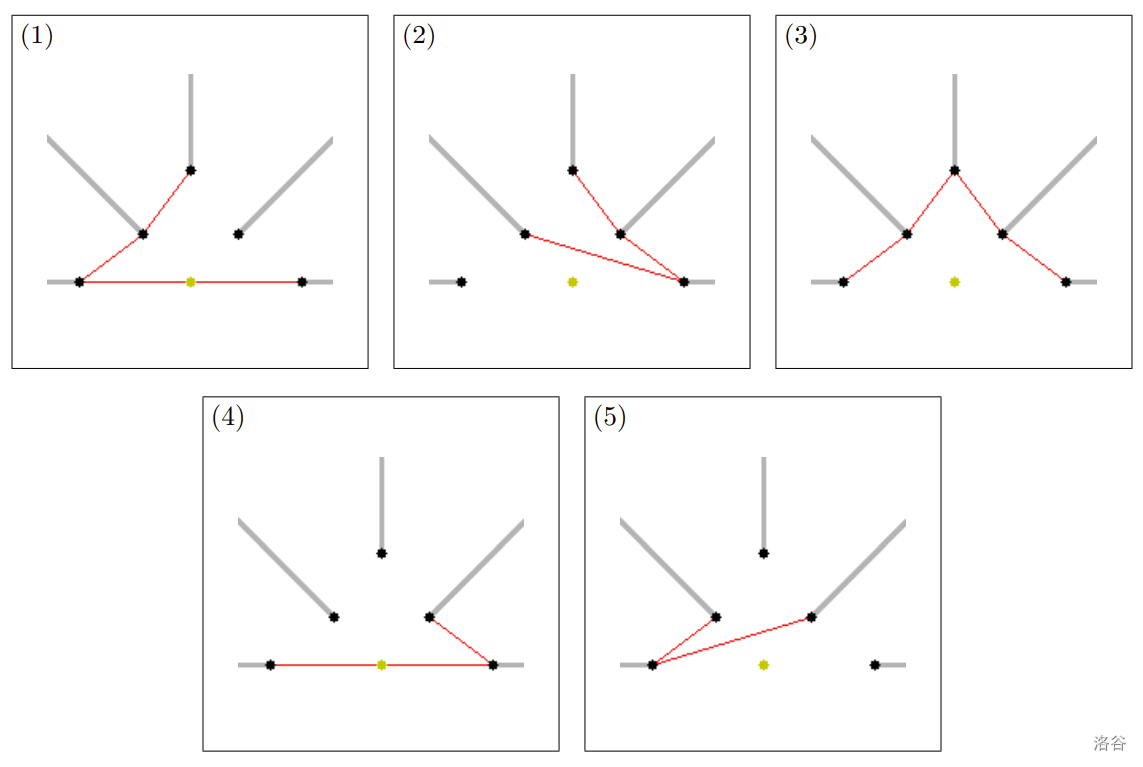
图 F.1. 样例输入 1 中前五对集合的最短路线。黑点是杆子的位置，灰线是它们的阴影。黄棕色的点是点光源的位置。对于每个图，红线表示从初始小车位置到目的地的最短路线。 :::

翻译由 DeepSeek V3 完成