Description

ICPC（极其宏大且特别舒适）剧院正在举办一系列传统活动来庆祝新年！

每个活动都有其固定的持续时间。活动的开始时间可以灵活安排，只要没有两个活动时间重叠。一个活动可以在另一个活动结束后立即开始。

活动的开始时间会影响其成本。活动的成本由其开始时间的连续分段线性函数（折线函数）给出。不同的活动可能有不同的成本函数。

你需要安排所有活动，使得总成本最小。

Input Format

输入由单个测试用例组成，格式如下。

$$\begin{aligned} &n \\ &\text{Description}_1 \\ &\vdots \\ &\text{Description}_n \end{aligned}$$

第一行包含一个整数 $n$，表示活动的数量。满足 $2 \leq n \leq 11$。接下来是活动的描述。第 $i$ 个活动 ($1 \leq i \leq n$) 的描述 $\text{Description}_i$ 格式如下。

$$\begin{aligned} &m \ l \\ &x_1 \ y_1 \\ &\vdots \\ &x_m \ y_m \end{aligned}$$

第一行的整数 $m$ 是该活动成本函数的顶点数。同一行的整数 $l$ 是该活动的持续时间。满足 $1 \leq m \leq 60$ 和 $1 \leq l \leq 10^8$。

接下来的 $m$ 行描述成本函数。这 $m$ 行中的第 $j$ 行由两个整数 $x_j$ 和 $y_j$ 组成，指定了成本函数的第 $j$ 个顶点。满足 $0 \leq x_1 < \cdots < x_m \leq 10^8$ 和 $0 \leq y_j \leq 10^8$。此外，对于任意 $1 \leq j < m$，$(y_{j+1} - y_j)/(x_{j+1} - x_j)$ 是整数。

活动的开始时间 $t$ 必须满足 $x_1 \leq t \leq x_m$。对于满足 $x_j \leq t \leq x_{j+1}$ 的 $j$ ($1 \leq j < m$)，活动的成本由 $y_j + (t - x_j) \times (y_{j+1} - y_j)/(x_{j+1} - x_j)$ 给出。

所有成本函数的顶点总数不超过 60。

Output Format

在一行中输出可能的最小总成本。

保证至少存在一个没有重叠的可能安排。可以证明答案是整数。

3
3 50
300 2500
350 0
400 3000
2 120
380 0
400 2400
4 160
0 800
400 0
450 100
950 4600

1460

4
2 160
384 0
1000 2464
3 280
0 2646
441 0
1000 2795
1 160
544 0
2 240
720 0
1220 2000

2022

Hint

对于样例输入 1，将三个活动的（开始时间，结束时间）对分别设为 $(330, 380)$、$(380, 500)$ 和 $(170, 330)$，可以在没有活动重叠的情况下实现最小总成本。活动 1 的成本为 $2500 + (330 - 300) \times (0 - 2500)/(350 - 300) = 1000$。类似地，活动 2 和 3 的成本分别为 $0$ 和 $460$。

对于样例输入 2，四个活动的最小成本安排为 $(384, 544)$、$(104, 384)$、$(544, 704)$ 和 $(720, 960)$。

:::align{center}

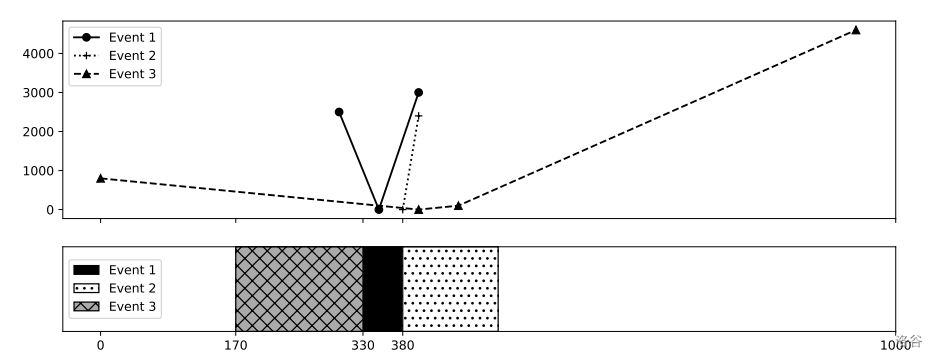
图 K.1. 样例输入 1 的成本函数及一个示例安排

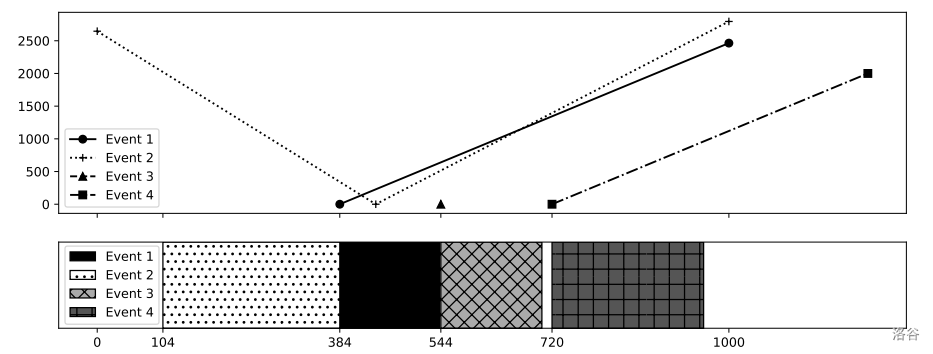
图 K.2. 样例输入 2 的成本函数及一个示例安排 :::

在图 K.1 和 K.2 中，上部图中的折线表示成本函数，下部图中的矩形表示实现最小总成本的安排中的活动持续时间。

翻译由 DeepSeek V3 完成