Description

一位著名的占卜师将为你预测命运。她有一些塔罗牌和一个六面骰子。她将使用骰子按以下方式选择一张牌，那张牌将揭示你的未来。

初始时，这些牌从左到右排成一行。骰子被投掷，以等概率显示 $1$ 到 $6$ 中的一个数字。当骰子显示的数字为 $x$ 时，从左数的第 $x$ 张牌以及其后每隔六张牌（即第 $(x + 6k)$ 张牌，$k = 0, 1, 2, \ldots$）将被移除，然后剩余的牌向左滑动以填补空缺。注意，如果剩余牌的数量少于 $x$，则不移除任何牌。这个移除和滑动的过程重复进行，直到只剩下一张牌。

图 G.1 展示了当骰子显示 $2$ 时牌如何被移除和滑动。

:::align{center}

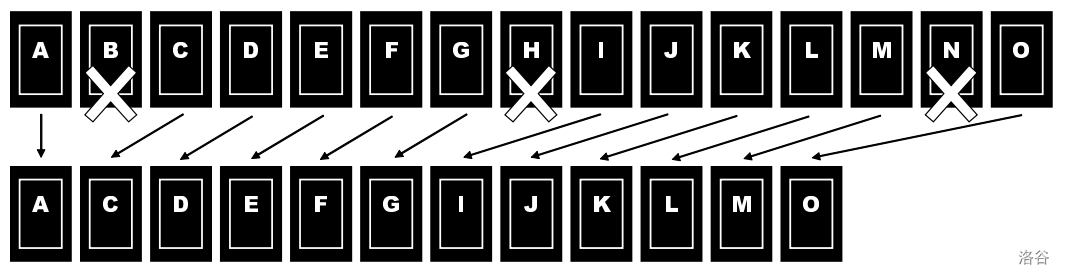
图 G.1. 牌的移除和滑动 :::

你被给予初始塔罗牌的数量。对于最初放置的每一张牌，计算该牌最终留存的概率。

Input Format

输入是一行，包含一个整数 $n$，表示塔罗牌的数量，其范围在 $2$ 到 $3 \times 10^5$ 之间（含）。

Output Format

输出 $n$ 行，第 $i$ 行应为一个整数，该整数根据从左数第 $i$ 张牌最终留存的概率按以下方式确定。

3

332748118
332748118
332748118

7

305019108
876236710
876236710
876236710
876236710
876236710
305019108

8

64701023
112764640
160828257
160828257
160828257
160828257
112764640
64701023

Hint

对于样例输入 1，所有牌最终留存的概率相等，均为 $1/3$。

对于样例输入 2，让我们考虑最左边牌最终留存的概率。要使这种情况发生，骰子第一次显示的数字不能是 $1$。在得到一个非 $1$ 的数字后，将剩下六张牌。这六张牌最终留存的概率相同。由此观察，最左边牌最终留存的概率计算为 $(5/6) \times (1/6) = 5/36$。同样的推理适用于最右边的牌。对于其余牌，概率相等，为 $(1 - 2 \times 5/36)/5 = 13/90$。