#P14790. [NERC 2025] Irrigation Interlock
[NERC 2025] Irrigation Interlock
Description
两个灌溉合作社共享同一片肥沃的谷地。第一个合作社维护着分布在田野中的泵站;第二个合作社监管着周围山上的水库。每当两个合作社决定铺设一对新管道时,这些管道必须相交——在相交处他们可以安装一个联合阀门。管道始终沿着连接一对不同泵站或一对不同水库的直线段铺设。如果两条管道至少共享一个公共点(接触和重叠的管道被视为相交),则认为它们相交。
你将在笛卡尔平面上获得每个泵站和每个水库的精确坐标。针对每个规划场景,判断第一个合作社是否能选择两个不同的泵站,第二个合作社是否能选择两个不同的水库,使得连接这两对点的直线管道相交。如果可能,报告这些泵站和水库的索引;否则声明该项目无法实现。
Input Format
第一行包含一个整数 () —— 规划场景的数量。
对于每个规划场景:
- 第一行包含一个整数 () —— 第一个合作社管理的泵站数量。
- 接下来的 行,每行包含两个整数 和 () —— 泵站 的笛卡尔坐标。泵站的位置互不相同。
- 接下来一行包含一个整数 () —— 第二个合作社管理的水库数量。
- 接下来的 行,每行包含两个整数 和 () —— 水库 的笛卡尔坐标。水库的位置互不相同。
没有任何泵站与任何水库位置相同。
保证所有规划场景的 之和不超过 ,所有规划场景的 之和也不超过 。
Output Format
对于每个规划场景:
- 如果第一个合作社可以选择两个泵站,第二个合作社可以选择两个水库,使得连接每对点的直线管道相交,则输出四个整数 —— 两个所选泵站的索引 () 和两个所选水库的索引 ()。
- 如果这样的相交不可能,则输出 。
- 如果存在多个有效解决方案,输出其中任意一个即可接受。
3
4
0 0
4 0
3 3
1 3
5
-1 1
5 1
2 -1
2 4
6 3
4
0 0
1 0
0 1
1 1
4
5 5
6 5
5 6
6 6
3
0 0
4 0
0 2
3
4 -2
4 2
6 1
1 4 1 2
-1
1 2 1 2
Hint
:::align{center}
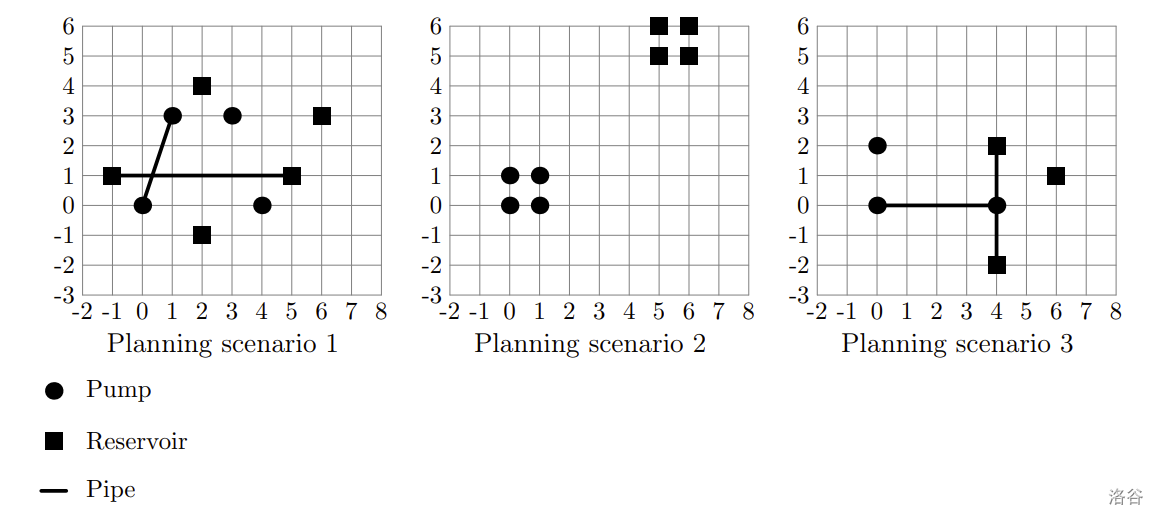 :::
:::

 京公网安备 11011102002149号
京公网安备 11011102002149号