Description

存在一个三角形，其三个顶点 $A$、$B$、$C$ 的坐标均为整数。如果你在三角形的每条边上各选取一个坐标为整数的点，并将这些点连接起来，就会形成一个新的三角形。在创建新三角形时，不能选取给定三角形的顶点作为新三角形的顶点。

根据你选取和连接的点的不同，新创建的三角形的面积可能较大也可能较小。

你需要编写一个程序，找出新三角形可能的最大面积和最小面积（如果它们存在的话）。

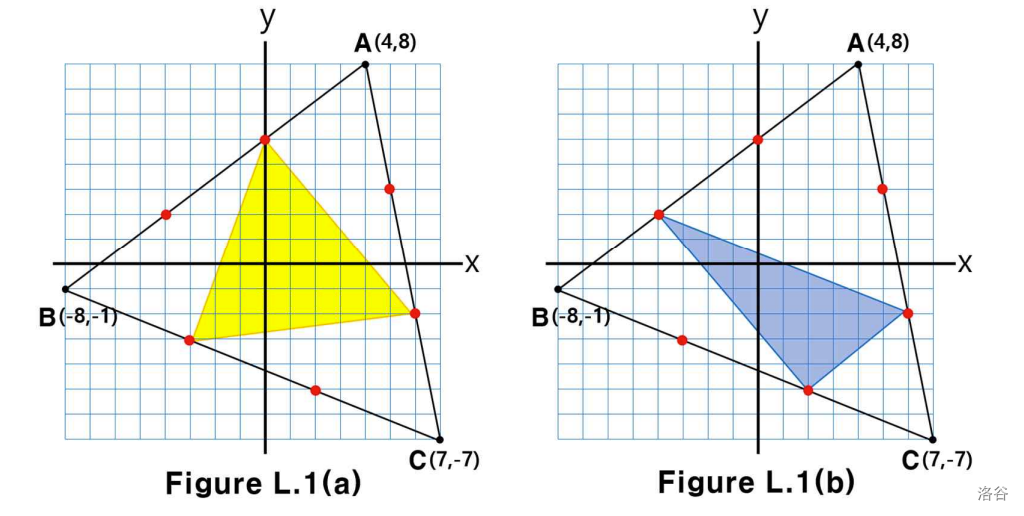
例如，如下图所示，如果给定三角形的三个顶点坐标为 $(4,8)$、$(-8,-1)$ 和 $(7,-7)$，那么图 L.1(a) 中所示的黄色三角形是满足条件的三角形中面积最大的，而图 L.1(b) 中所示的蓝色三角形是面积最小的。

:::align{center} :::

可能在给定三角形的某些边上不存在坐标为整数的点，这种情况下，你所寻找的三角形就不存在。

保证输入的三个点不共线。

Input Format

你的程序需要从标准输入读取数据。输入包含一行，包含六个整数，分别是一个三角形的三个顶点 $A = (A_x, A_y)$、$B = (B_x, B_y)$、$C = (C_x, C_y)$ 的 $(x, y)$ 坐标，按顺序依次给出 $A_x$、$A_y$、$B_x$、$B_y$、$C_x$、$C_y$。每个坐标值都是介于 $-10^9$ 到 $10^9$ 之间（含）的整数。

Output Format

你的程序需要向标准输出写入结果。设新创建的三角形中面积最大的面积为 $S_{\text{max}}$，面积最小的面积为 $S_{\text{min}}$。如果这样的三角形可以找到，则按顺序输出 $2S_{\text{max}}$ 和 $2S_{\text{min}}$，其中 $2S_{\text{max}}$ 和 $2S_{\text{min}}$ 均为正整数。如果这样的三角形无法找到，则输出 $-1$。

4 8 -8 -1 7 -7

69 46

-8 1 7 11 7 -5

121 23

0 0 1 10 10 0

-1