Description

乔三世国王陵墓是一座巨大的石头建筑，呈直方图形状。直方图是一个简单的直边多边形，其边界由两条链组成：一条是相对于水平轴单调的上链，另一条是水平线段的下链，称为基线段（见图 E.1）。

:::align{center} :::

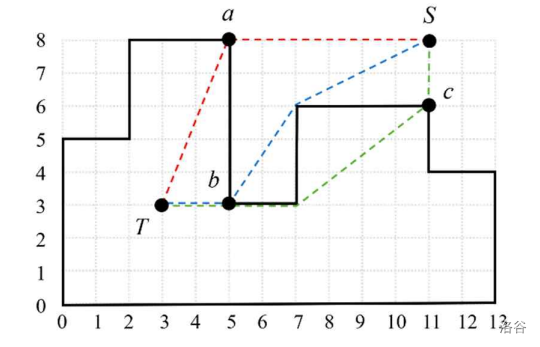传闻有一处隐藏的宝藏位于这座陵墓内的某个地方。著名的宝藏猎人梅特里发现了宝藏位于点 $T$。梅特里的计划是凿穿陵墓的墙壁，进入内部并取回宝藏。她将从陵墓外的一个特定位置 $S$ 开始。利用她的设备，梅特里只能凿穿一个点，该点对应于陵墓边界上的一个顶点。由于在所有顶点凿穿墙壁所需的时间相同，因此最小化所用时间的关键在于找到从 $S$ 到 $T$ 的最短路径。

图 E.1 展示了一座陵墓以及从 $S$ 到 $T$ 的几条可能路径，这些路径只穿过一个顶点。穿过顶点 $a$ 的路径总长度为 $11.385165 = 6 + \sqrt{29}$，穿过顶点 $b$ 的路径长度为 $10.077687 = \sqrt{20} + \sqrt{13} + 2$，穿过顶点 $c$ 的路径长度为 $11.0 = 2 + \sqrt{25} + 4$。其中，最短路径是穿过顶点 $b$ 的路径。

给定陵墓的边界以及 $S$ 和 $T$ 的位置，请编写一个程序，找到从 $S$ 到 $T$ 且仅穿过一个顶点的最短路径的长度。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含一个整数 $n$ ($4 \leq n \leq 100,000$)，其中 $n$ 为偶数，表示代表陵墓的直方图的顶点数。第二行给出 $n$ 个整数 $v_1, v_2, \ldots, v_n$ ($v_1 = v_n = 0$, $0 \leq v_i \leq 10^6$)，它们表示垂直边的 x 坐标和水平边的 y 坐标。沿着直方图的上链，从基线段的左端到右端，垂直边和水平边交替出现。每条边的长度至少为 $1$，且 x 坐标按严格递增的顺序给出。最后一行包含四个整数 $s_x, s_y, t_x, t_y$ ($-10^6 \leq s_x, s_y \leq 2 \times 10^6$, $0 < t_x, t_y < 10^6$)，其中 $(s_x, s_y)$ 和 $(t_x, t_y)$ 分别对应点 $S$ 和 $T$。注意 $S$ 是直方图外部的一个点，$T$ 是直方图内部的一个点，两者均不位于边界上。

Output Format

你的程序需要向标准输出写入结果。输出恰好一行。该行应包含一个实数值，即从 $S$ 到 $T$ 的最短路径的长度。你的输出 $z$ 应采用整数部分、小数点和小数部分的格式，并且如果满足 $a - 10^{-3} < z < a + 10^{-3}$，则被认为是“正确的”，其中 $a$ 表示出题人的答案。两点 $p = (x_1, y_1)$ 和 $q = (x_2, y_2)$ 之间的欧几里得距离为 $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$。

12
0 5 2 8 5 3 7 6 11 4 13 0
11 8 3 3

10.077687

8
0 7 2 2 5 7 7 0
-2 4 6 4

11.767829

4
0 5 8 0
8 6 4 2

6.0

Hint

翻译由 DeepSeek V3 完成