Description

有一条笔直的道路，两种类型的有轨电车在上面运行。一种是从东向西行驶的电车，另一种是从西向东行驶的电车。每种类型的电车都有多班定期运行，因此任何人都可以在任何时间乘坐任意方向的电车。要乘坐电车，你需要为每次乘坐的方向支付车票。换句话说，要乘坐从东向西移动的电车，你必须支付一张 西行车票；反之，要乘坐从西向东移动的电车，你必须支付一张 东行车票。你可以在任何时间、任何地点上下车，并且一旦上车，你可以想坐多久就坐多久。

Bob 是一名邮局工作人员，他每天去邮局投递分配给他的邮件。他使用电车来投递。为了方便起见，每个需要投递邮件的地点用一个 $x$ 坐标表示，而邮局位于 $x = 0$。

为了投递 $n$ 封邮件，邮局给了 Bob $n$ 张电车票。Bob 使用一张票来投递一封邮件。然而，在邮局提供的 $n$ 张票中，西行车票的数量是 $w$，东行车票的数量是 $e$ ($e = n - w$)。Bob 希望利用他在邮局收到的这些票，不仅规划出这 $n$ 封邮件的投递顺序，还要最小化他乘坐电车所旅行的总距离。

根据邮件投递顺序的不同，可以分为两种类型。第一种类型，记作 $t = 1$，表示邮件的投递顺序不重要。第二种类型，记作 $t = 2$，表示有一封特定的指定邮件必须在最后投递，而其他所有邮件的投递顺序可以任意。

例如，假设 $n = 5$，$w = 4$ (西行车票的数量)，$t = 2$，需要投递邮件地点的 $x$ 坐标是 $(-20, -15, 20, 30, 10)$，并且必须最后投递的特定邮件的 $x$ 坐标是 $x = 10$。最优的投递路线如图 H.1 所示，乘坐电车移动的总距离是 90。如图 H.1 所示，使用了四张 西行车票 和一张 东行车票，并且指定邮件在最后被投递。

:::align{center} :::

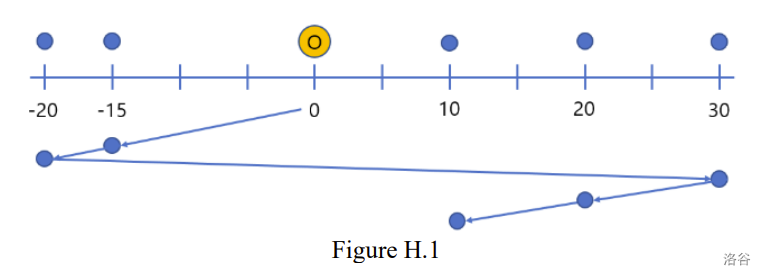考虑另一个例子，除了 $t = 1$ 以外，所有信息都与上面相同。这种情况下的最优投递路线如图 H.2 所示，总距离是 80。在这种情况下，你可以看到同样使用了四张 西行车票 和一张 东行车票。

:::align{center} :::

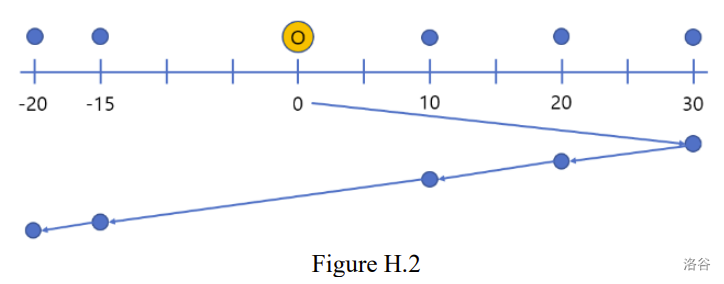给定关于 Bob 需要投递的邮件的信息，编写一个程序，求出他乘坐电车所需旅行的最小距离。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含三个整数 $n$, $w$ 和 $t$ ($1 \leq n \leq 3 \times 10^5$, $0 \leq w \leq n$, $1 \leq t \leq 2$)，其中 $n$ 是邮件的数量，$w$ 是 西行车票 的数量，$t$ 表示如上所述的投递顺序类型。注意，东行车票的数量是 $n - w$。接下来的一行给出 $n$ 个整数。第 $i$ 个整数 $x_i$ ($1 \leq i \leq n$, $-10^9 \leq x_i \leq 10^9$, $x_i \neq 0$) 是第 $i$ 封邮件需要投递地点的 $x$ 坐标。当 $t = 2$ 时，$x_n$ 表示必须最后投递的特定邮件的 $x$ 坐标。

你可以假设没有两个 $x_i$ 是相同的。

Output Format

你的程序需要向标准输出写入结果。输出恰好一行。该行应包含 Bob 投递所有邮件所需旅行的最小距离。如果 Bob 无法使用这些车票完成投递，则输出 $-1$。

5 4 2
-20 -15 20 30 10

90

5 4 1
-20 -15 20 30 10

80

7 1 2
10 13 -30 24 50 -5 -21

-1

Hint

翻译由 DeepSeek V3 完成