Description

给定一组相互交往的人，我们可以定义一个图：图的顶点是人，如果两个人是朋友，则他们之间有一条边。这样的图被称为社交网络，可以定义在任何人群集合上，例如一所大学的学生或一个小镇的居民。近年来，一门分析社交网络的全新科学已经兴起，因为关于人及其行为的许多有趣方面，最好通过友谊图的性质来理解。

给定一个友谊图，其中顶点是“问题求解”课程中的学生，你的任务是编写一个程序，将班级中的学生分解为两个小组 $A$ 和 $B$，使得以下三个条件同时满足：

• 班级中的每个学生恰好属于一个小组，$A$ 或 $B$。
• 每个小组中的任意两个学生互为朋友。
• 两个小组的规模之差 $||A| - |B||$ 尽可能小。

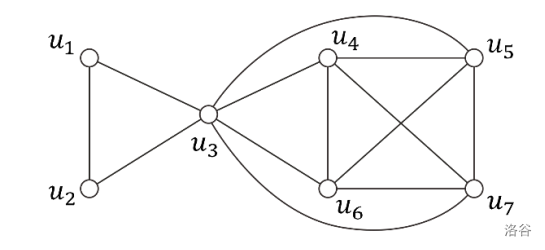
例如，假设给定如下图所示的友谊图。将学生分解为 $A = \{u_1, u_2, u_3, u_6\}$ 和 $B = \{u_4, u_5, u_7\}$ 是不可能的，因为 $u_2$ 和 $u_6$ 不是朋友。另一方面，在分解为 $A = \{u_1, u_2\}$ 和 $B = \{u_3, u_4, u_5, u_6, u_7\}$ 时，每个小组中的任意两个学生互为朋友；然而，两个小组的规模之差（$|2 - 5| = 3$）大于分解为 $A = \{u_1, u_2, u_3\}$ 和 $B = \{u_4, u_5, u_6, u_7\}$ 时的差值（$|3 - 4| = 1$）。最后一种分解就是我们想要的最优分解。

:::align{center} :::

Input Format

你的程序需要从标准输入读取数据。第一行包含两个整数 $n$ 和 $m$，分别表示友谊图的顶点数和边数，其中 $2 \leq n \leq 1,000$，$0 \leq m \leq \binom{n}{2}$。顶点编号从 $1$ 到 $n$。接下来的 $m$ 行中，每行包含两个整数 $u$ 和 $v$，表示图中的一条边 $(u, v)$。

Output Format

你的程序需要向标准输出写入数据。输出恰好一行，包含一个整数。如果可以将学生分解为满足上述三个条件的两个小组，则该整数应为两个小组规模之差的最小值；否则，该整数应为 $-1$。

7 13
1 2
2 3
3 1
3 4
3 5
3 6
3 7
4 5
5 7
7 6
6 4
4 7
5 6

1

5 5
1 2
2 3
3 4
4 5
5 1

-1

4 4
4 3
3 2
2 1
1 4

0

Hint

翻译由 DeepSeek V3 完成