Description

一只青蛙住在一个美丽的湖中。湖面上有许多荷叶排成一行漂浮着，这些荷叶用直线上的闭区间表示。青蛙喜欢待在荷叶上，并在它们之间移动。

给定直线上（即 $x$ 轴上）表示荷叶的 $n$ 个闭区间，青蛙初始位于某个区间 $I_0$ 上。如果两个区间重叠，青蛙可以从一个区间 $I$ 移动到另一个区间 $J$。两个区间重叠当它们共享一个公共点。因此，青蛙可以通过重叠的区间移动。当青蛙通过重叠区间向右（左）移动时，它可能会到达一个区间 $H$，此时它无法再从 $H$ 的右（左）端点向右（左）移动。在这种情况下，如果存在满足以下条件的区间 $K$：其左（右）端点大于（小于）$H$ 的右（左）端点，并且在其左（右）端点最小（最大）的区间中，青蛙可以跳转到区间 $K$。然后，跳跃长度定义为 $H$ 的右（左）端点与 $K$ 的左（右）端点之间的距离。参见图 F.1。

:::align{center}

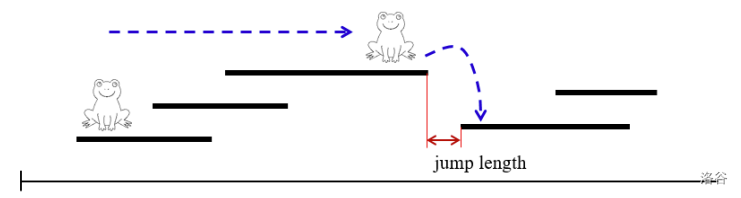
图 F.1 跳跃长度 :::

给定一个由 $k$ 个区间 $I_1, I_2, \dots, I_k$ 组成的序列，青蛙需要从初始区间 $I_0$ 出发，按顺序访问这些区间。在此旅行中，青蛙在必要时必须进行跳跃。

例如，在图 F.2 中，给出了八个区间 $[1,8]$、$[2,4]$、$[5,11]$、$[13,15]$、$[15,17]$、$[16,18]$、$[19,22]$ 和 $[20,22]$，并从 $1$ 到 $8$ 编号。青蛙初始位于区间 $1$。给定青蛙需按顺序访问的区间序列：$3$、$7$、$4$、$6$、$3$。那么青蛙从区间 $1$ 移动到 $3$ 时没有跳跃，从区间 $3$ 移动到 $7$ 时有两次跳跃，即 $3 \to 4$ 和 $6 \to 7$，跳跃总长度为 $3$。在此移动过程中，青蛙经过了区间 $4$。然而，它需要在访问区间 $7$ 之后再访问区间 $4$。然后，从区间 $7$ 到 $4$ 以及从 $6$ 到 $3$ 的移动过程中有两次跳跃，跳跃总长度为 $3$。因此，在青蛙访问完所有给定区间后，总跳跃长度为 $6$。

:::align{center} :::

给定直线上的 $n$ 个区间以及一个由 $k$ 个区间组成的序列，请编写一个程序，输出青蛙从初始区间 $1$ 出发按顺序访问这 $k$ 个区间的旅行过程中总跳跃长度。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ 和 $k$ ($1 \leq n \leq 100,000$ 且 $1 \leq k \leq 1,000,000$)，其中 $n$ 是区间数量，$k$ 是青蛙需要访问的区间数量。区间从 $1$ 到 $n$ 编号，青蛙的初始位置始终是区间 $1$。接下来的 $n$ 行中，第 $i$ 行包含两个整数 $a$ 和 $b$ ($0 \leq a < b \leq 10^9$)，分别表示区间 $i$ 的左端点和右端点。区间按其左端点递增的顺序给出——如果左端点相同，则按右端点递增顺序给出。此外，所有区间互不相同。接下来的一行包含 $k$ 个整数，表示青蛙按顺序需要访问的区间。这些整数在 $1$ 到 $n$ 之间，可以重复。

Output Format

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含青蛙按顺序访问给定的 $k$ 个区间时的总跳跃长度。

4 3
0 2
0 3
3 5
6 7
4 2 3

2

4 3
0 2
0 3
3 5
6 7
2 3 2

0

8 5
1 8
2 4
5 11
13 15
15 17
16 18
19 22
20 22
3 7 4 6 3

6