Description

有一根可折叠的棍子，由 $n$ 段长度为正的节段组成。节段之间通过铰链（可伸缩的细绳）连接，允许每段在铰链处折叠 $180$ 度。缠绕长度 是指棍子在一个或多个铰链处折叠后折叠部分的长度。根据折叠策略的不同，缠绕长度可能不同。

你需要在以下折叠方式的条件下找到最小的缠绕长度：首先，将棍子的各节段沿水平线放置。然后，从左到右顺时针折叠棍子。在折叠过程中，每个铰链左侧所连接的节段要么顺时针旋转 $180$ 度，要么完全不旋转。

例如，下图展示了一根四节段的棍子，节段长度总和为 $10$。图中，从左到右各节段的长度分别为 $3$、$2$、$2$ 和 $3$，铰链标记为 ①、②、③。

:::align{center} :::

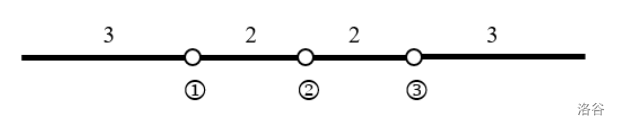在此例中，棍子不能在铰链 ① 和 ② 处同时折叠。这是因为如果先在铰链 ① 处折叠，再在铰链 ② 处折叠，经过铰链 ② 的长度为 $3$ 的节段将被折断。如果仅在铰链 ② 处折叠，缠绕长度为 $5$。如果依次在铰链 ① 和 ③ 处折叠，缠绕长度为 $4$，如下图所示。

:::align{center} :::

给定一根可折叠棍子的节段长度序列，请编写程序输出该棍子的最小缠绕长度。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含一个整数 $n$ ($2 \leq n \leq 100,000$)，其中 $n$ 是可折叠棍子的节段数。第二行包含 $n$ 个正整数，表示从棍子最左端到最右端的节段长度序列。每段长度不超过 $20,000$。

Output Format

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含一个正整数，表示最小缠绕长度。

4
3 2 2 3

4

5
1 1 1 1 1

1

7
1 3 2 3 4 2 2

6

Hint

翻译由 DeepSeek V3 完成