Description

ICPC 王国决定建造一座新的城堡。城堡的边界被设计为一个直角多边形，其边平行于 $x$ 轴或 $y$ 轴。为了最小化暴露在敌人攻击下的损害，王国希望最小化该直角多边形的周长。让我们进一步详细说明。

一个具有 $n$ 个整数坐标顶点的直角多边形 $P$ 实现 了一个长度为 $n$、由字母 L 和 R 组成的转向序列 $S$，如果存在一种沿 $P$ 边界逆时针的遍历，使得在遍历过程中遇到的 $P$ 的顶点处的转向构成了转向序列 $S$；在凸顶点处的左转对应 L，在凹顶点处的右转对应 R。例如，图 B.1(a) 中的直角多边形实现了长度为 $16$ 的转向序列 $S = \text{RLLRLLLLRRLRIRLLL}$。另一个长度为 $14$ 的转向序列 $S = \text{LLRLLRLLRLLRLLR}$ 可以由图 B.1(b) 和 B.1(c) 中的直角多边形实现。请注意，一个转向序列在整数平面上可以有无限多个直角多边形实现。

一个多边形如果是简单的，则除了相邻边的端点外，没有两条边相交。一个多边形如果相对于某个坐标轴是单调的，则其与垂直于该轴的直线的交点最多为一个线段。单调多边形如果同时相对于 $x$ 轴和 $y$ 轴都是单调的，则称为 2-单调；如果仅相对于一个轴是单调的，而相对于另一个轴不是，则称为 1-单调。例如，图 B.1(a) 中的多边形是 1-单调的，因为它仅对 $x$ 轴单调；而图 B.1(b) 和 B.1(c) 中的多边形是 2-单调的。一个转向序列也被称为 $t$-单调，如果任何实现该转向序列的简单直角多边形都是 $t$-单调的，其中 $t = 1, 2$。

:::align{center}

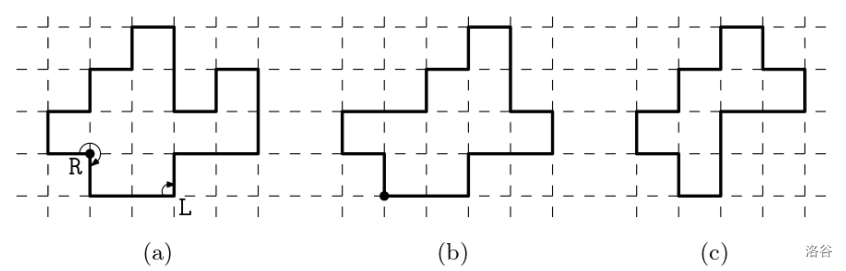
图 B.1 (a) 一个实现 1-单调转向序列 RLLRLLLRRLLRIRLLL 的简单 1-单调直角多边形（从标记顶点开始）。(b) 一个实现 2-单调转向序列 LLRLLRLLRLLRLLR 的简单 2-单调直角多边形（从标记顶点开始）。(c) 对于 (b) 中的转向序列，具有最小周长的 2-单调直角多边形。 :::

直角多边形的周长是其各边长度的总和。图 B.1(b) 中多边形的周长是 $18$，但这不是 $\text{LLRLLRLLRLLRLLR}$ 的最小周长。其最小周长应为 $16$，如图 B.1(c) 所示。

给定一个长度为 $n$ 的 $t$-单调转向序列（$t = 1, 2$），请编写一个程序，计算能够实现该输入 $t$-单调转向序列的简单 $t$-单调直角多边形的最小周长。

Input Format

你的程序需要从标准输入读取数据。输入是一行，包含一个由大写字母 L 和 R 组成的长度为 $n$ 的转向序列字符串，它是一个 $t$-单调转向序列，其中 $t = 1, 2$，且 $4 \leq n \leq 10^{t+3}$。

Output Format

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含一个正整数，表示能够实现输入 $t$-单调转向序列（$t = 1, 2$）的简单 $t$-单调直角多边形的最小周长。

LLRLLRLLRLRLLR

16

RLLRLLLRRLLRLRLL

20

LLRRLLLLRRLL

16

RLLRLLRLLRLL

12

Hint

翻译由 DeepSeek V3 完成