Description

众所周知，平面上两个不相交（既不重叠也不相切）的圆有 四条不同的公切线。

:::align{center} :::

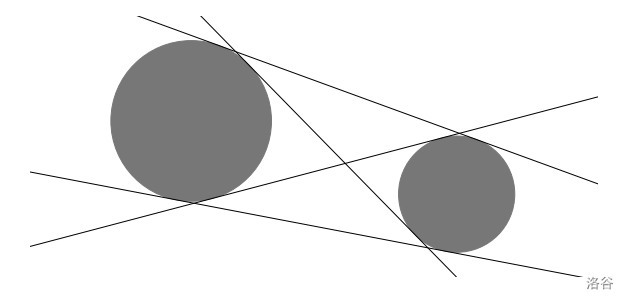给定 $xy$ 平面上的四条直线。你的目标是：对这些直线施加平行移动，使得它们成为某对半径为正且不相交的圆的四条不同的公切线。你希望以尽可能低的 成本 完成此操作，其中成本定义为平移距离的总和。一条直线的平移距离是其平移前后两直线之间的距离。

每条直线由两个参数 $a$ 和 $d$ 指定，并由以下方程定义：

$$x \cos\left(\frac{\pi a}{180}\right) + y \sin\left(\frac{\pi a}{180}\right) = d.$$

例如，参数为 $(a, d) = (60, 1)$ 的直线代表 $x/2 + \sqrt{3}y/2 = 1$，因为 $\cos(\pi/3) = 1/2$ 且 $\sin(\pi/3) = \sqrt{3}/2$。

首先，判断目标是否可达。如果可达，确定 最小所需成本，其定义如下：最小的值 $c$，使得对于任意正实数 $\varepsilon$，都能以不超过 $c + \varepsilon$ 的成本实现目标。目标不必以恰好等于 $c$ 的成本实现。

Input Format

输入包含一个或多个测试用例。输入的第一行包含一个整数 $t$ ($1 \le t \le 1000$)，表示测试用例的数量。接下来是 $t$ 个测试用例的描述，每个用例的格式如下。

$$a_1\ d_1$$ $$\vdots$$ $$a_4\ d_4$$

对于 $i = 1, \ldots, 4$，两个整数 $a_i$ 和 $d_i$ 是用于指定第 $i$ 条直线的参数 ($0 \le a_i < 180$， $-1000 \le d_i \le 1000$)。在平移之前，两条或多条直线可能相同。

Output Format

对于每个测试用例，如果目标不可达，则输出一行 $no$。否则，输出一行上述定义的最小所需成本。输出的绝对或相对误差必须小于等于 $10^{-7}$。

4
90 0
90 0
45 0
135 0
0 -200
0 100
30 0
150 0
120 100
120 75
30 50
30 -100
178 -132
144 -83
165 199
19 31

0
86.602540378444
no
173.814220263386

Hint

在样例输入 1 的第一个测试用例中，你至少需要移动前两条相同的直线之一（图 L.1 (a)）。对于任意 $\varepsilon > 0$，将其中一条直线沿 $y$ 轴正方向平移 $\varepsilon/2$，另一条沿 $y$ 轴负方向平移 $\varepsilon/2$，即可在成本为 $\varepsilon$ 的情况下实现目标。这将产生半径为 $\varepsilon/2$ 的圆的四条公切线（图 L.1 (b)）。由于 $\varepsilon$ 可以任意小，最小所需成本为 $0$。其余情况如图 L.1 (c) 至 (e) 所示。

:::align{center}

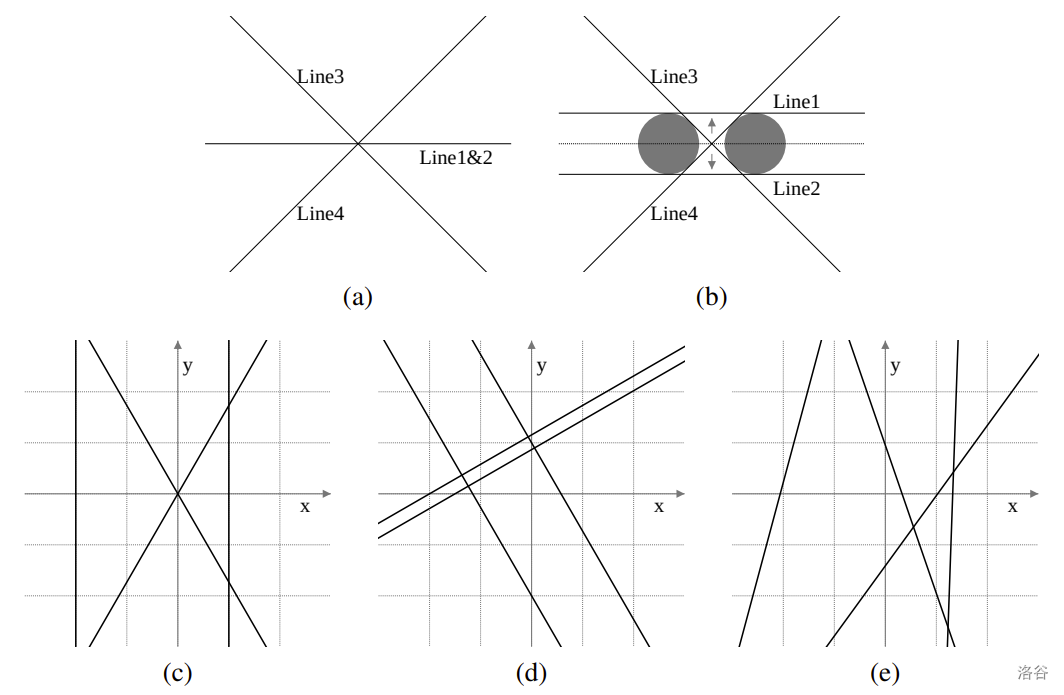
图 L.1. 样例输入 1 图示 :::

翻译由 DeepSeek V3 完成