Description

作为一名年轻的天文学家，你对一组具有独特特征的恒星的空间排列很感兴趣。了解这一点可能有助于理解早期宇宙的宇宙学。为此，你可以使用一种专门的仪器进行测量。

该仪器使用其自身的三维笛卡尔坐标系，其中原点 $(0, 0, 0)$ 设在地球上，恒星的位置被建模为格点（所有坐标均为整数的点）。你已经知道所有感兴趣的恒星到地球的距离，但它们的方向未知。

在一次测量中，你指定两颗不同的恒星，仪器会报告它们之间的距离。请注意，仪器不会报告恒星的绝对或相对方向。

请在有限的测量次数内确定所有恒星对之间的距离。

交互

输入的第一行包含一个整数 $n$，表示感兴趣的恒星数量 ($2 \le n \le 100$)。恒星编号为 $1$ 到 $n$。第二行包含 $n$ 个整数。其中第 $i$ 个是恒星 $i$ 到原点的距离平方。保证所有恒星都有整数坐标，每个坐标在 $-4000$ 到 $4000$ 之间（含）。没有两颗恒星在同一位置。没有恒星位于原点。

读取这两行后，你可以开始测量。要测量恒星 $i$ 和 $j$ 之间的距离，请输出一行 "measure $i$ $j$"，其中 $i$ 和 $j$ 是 $1$ 到 $n$（含）之间的不同整数。作为响应，将有一行输入可用，其中包含一个表示恒星 $i$ 和 $j$ 之间距离平方的整数。你最多可以进行 $300$ 次测量。

当你确定了所有恒星对之间的距离后，请输出一行仅包含 answer 的行，然后按以下格式输出 $n-1$ 行。

这里，$d_{i,j}$ ($1 \le i < j \le n$) 是一个整数，表示恒星 $i$ 和 $j$ 之间的距离平方。请注意，你不需要确定恒星的坐标。输出这些行后，交互停止，你的程序必须终止，不再输出任何额外内容。

如果你的输出不符合上述规范，或者测量次数超过 $300$，你的提交将被判为错误答案。

恒星的坐标在交互开始前就已固定；交互期间不会改变。

我们提供了一个命令行工具供本地测试。更多详情，请参阅竞赛系统中的澄清说明。

3
1 11 4

14

11

9

measure 1 2

measure 2 3

measure 3 1

answer
14 9
11

4
47944017 47920034 47960009 47968006

answer
191728099 2 191824043
191760077 12
191856029

5
1 4 9 50 149

answer
5 10 45 162
13 38 181
29 206
371

Hint

在样例交互 1 中，恒星的坐标可以如下：

• 恒星 1 位于 $(1, 0, 0)$，
• 恒星 2 位于 $(-1, -1, 3)$，
• 恒星 3 位于 $(-2, 0, 0)$。

恒星 1 和 2 之间的距离是 $\sqrt{14}$。在第一次测量中，返回了距离平方 $14$。

:::align{center}

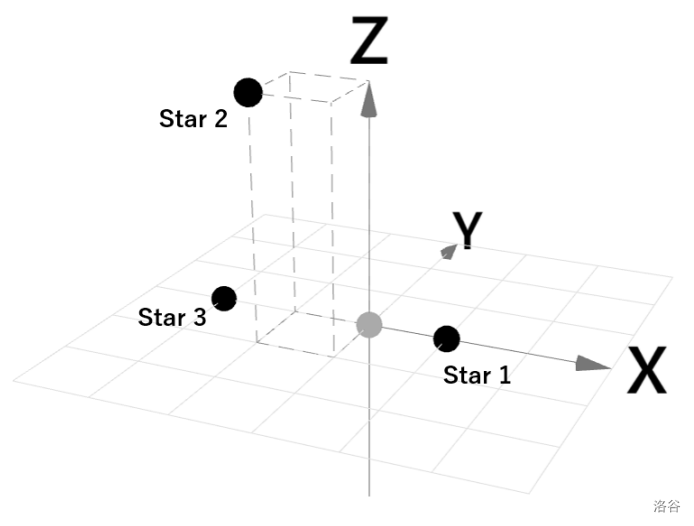
图 F.1. 样例交互 1 图示 :::

在样例交互 2 中，恒星的坐标可以如下：

• 恒星 1 位于 $(-3998, -3998, -3997)$，
• 恒星 2 位于 $(3997, 3997, 3996)$，
• 恒星 3 位于 $(-3999, -3998, -3998)$，
• 恒星 4 位于 $(3999, 3999, 3998)$。

在样例交互 3 中，恒星的坐标可以如下：

• 恒星 1 位于 $(1, 0, 0)$，
• 恒星 2 位于 $(0, -2, 0)$，
• 恒星 3 位于 $(0, 0, 3)$，
• 恒星 4 位于 $(3, -4, 5)$，
• 恒星 5 位于 $(-6, 7, -8)$。

翻译由 DeepSeek V3 完成