Description

在坐标平面的第一象限内，给定 $n$ 条平行于 $x$ 轴的线段。每条线段 $S_i$ ($1 \le i \le n$) 由其左端点和右端点的坐标表示，分别为 $(l_i, y_i)$ 和 $(r_i, y_i)$。所有坐标均为正整数。

现在你需要回答 $q$ 次询问。每次询问给定一条平行于 $y$ 轴的竖直线 $x = p$。这条竖直线由一个正整数 $p$ 表示。

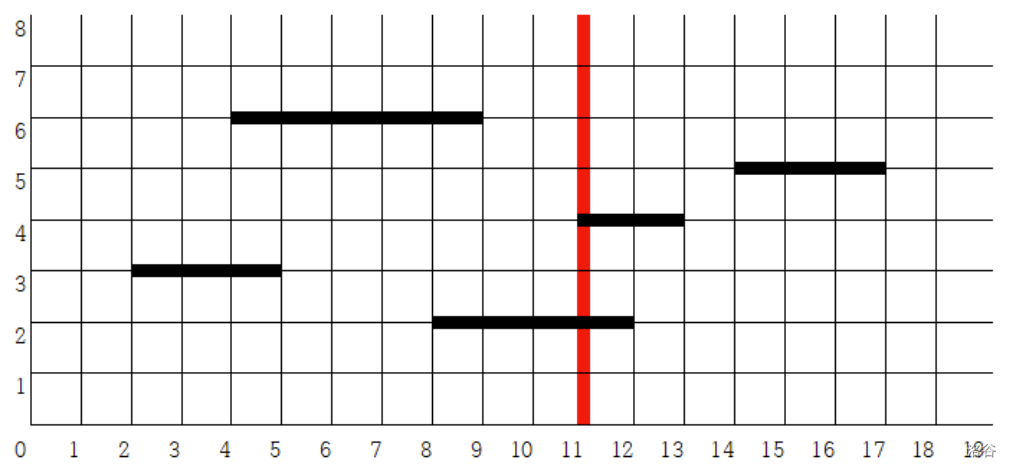
如果每条线段 $S_i$ 水平延伸，它最终会在点 $(p, y_i)$ 处与直线 $x = p$ 相交。如果该线段（包括其端点）已经与 $x = p$ 相交，则无需延伸。例如，假设有 $5$ 条线段 $\{(2,3), (5,3)\}$、$\{(4,6), (9,6)\}$、$\{(8,2), (12,2)\}$、$\{(11,4), (13,4)\}$ 和 $\{(14,5), (17,5)\}$，以及一条直线 $x = 11$。为了使每条线段都与 $x = 11$ 相交，第一条线段需要向右延伸 $6$，第二条线段向右延伸 $2$，第三条和第四条线段延伸 $0$，第五条线段向左延伸 $3$。

对于每次询问，确定所有线段与直线 $x = p$ 相交所需延伸长度的最大值。形式化地说，令 $\text{dist}(p, S_i)$ 表示线段 $S_i$ 需要延伸以在点 $(p, y_i)$ 处与 $x = p$ 相交的距离。对于每次询问，输出 $\max_{1 \le i \le n} \text{dist}(p, S_i)$。在上面的例子中，该询问的答案是 $6$。参见下图。

:::align{center} :::

给定 $n$ 条线段和 $q$ 次询问，请编写一个程序，输出每次询问对应的最大延伸长度。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含两个整数 $n$ ($1 \le n \le 2 \times 10^6$) 和 $q$ ($1 \le q \le 2 \times 10^6$)，其中 $n$ 是线段的数量，$q$ 是询问的次数。接下来的 $n$ 行中，第 $i$ 行包含三个整数 $l_i$、$r_i$ 和 $y_i$ ($1 \le l_i \le r_i \le 10^9$， $1 \le y_i \le 10^3$)，其中 $l_i$（对应地，$r_i$）是 $S_i$ 左（对应地，右）端点的 $x$ 坐标，$y_i$ 是 $S_i$ 两个端点的 $y$ 坐标。接下来的 $q$ 行是询问，第 $j$ 行包含一个整数 $p_j$ ($1 \le p_j \le 10^9$)，表示竖直线 $x = p_j$。

Output Format

你的程序需要向标准输出写入数据。对于每次询问，恰好输出一行。第 $j$ 行应包含所有线段在点 $(p_j, y_j)$ 处与 $x = p_j$ 相交所需延伸长度的最大值。

5 3
2 5 3
4 9 6
8 12 2
11 13 4
14 17 5
11
5
1

6
9
13

4 8
1 4 7
3 7 5
10 13 8
12 15 2
13
7
4
8
3
11
1
16

9
5
8
4
9
7
11
12

Hint

翻译由 DeepSeek V3 完成