Description

本题是关于 象限 的。什么是象限？让我们从平面 $\mathbb{R}^2$ 上任意两条互相垂直的直线 $\ell$ 和 $\ell'$ 开始。如果你从整个平面 $\mathbb{R}^2$ 中移除这两条直线 $\ell$ 和 $\ell'$，你将得到四个连通的、无界的区域。这四个区域中的每一个都称为一个 象限。请注意，象限的边界不属于它自身。

现在，考虑平面 $\mathbb{R}^2$ 上的一个点集 $P$。我们关心由点集 $P$ 定义的象限。具体地说，令 $\mathcal{Q}$ 为所有满足以下条件的象限 $Q$ 的集合：$Q$ 的边界恰好包含 $P$ 中的三个点。如果一个象限 $Q \in \mathcal{Q}$ 的内部恰好包含 $P$ 中的 $k$ 个点，则称 $Q$ 为一个 $k$-象限。下图展示了一个例子，其中点集 $P$ 由 14 个点（小圆圈）组成，你可以看到一个 5-象限 $Q \in \mathcal{Q}$（用青色阴影表示），其边界包含三个点 $p, q, r \in P$。

:::align{center} :::

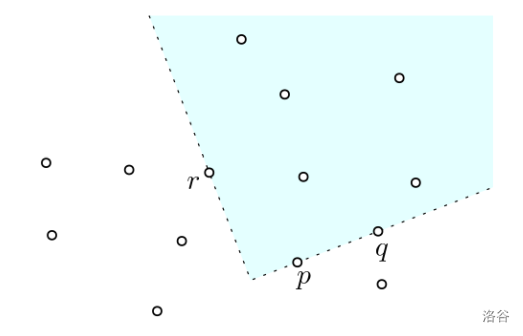给定一个包含 $n$ 个点的点集 $P$ 作为输入，请编写一个程序，计算对于每个 $0 \le k \le n-3$，$k$-象限的数量。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含一个整数 $n$ ($3 \le n \le 2,000$)，其中 $n$ 是输入点集 $P$ 中的点数。接下来的 $n$ 行中，每行给定两个整数 $x$ 和 $y$，均在 $-10^6$ 到 $10^6$ 之间（含），表示 $P$ 中一个输入点 $(x,y)$ 的 $x$ 坐标和 $y$ 坐标。你可以假设没有两个输入点具有相同的坐标，$P$ 中没有三点共线，并且平面 $\mathbb{R}^2$ 中不存在两条互相垂直的直线 $\ell$ 和 $\ell'$ 使得 $|\ell \cap P| \ge 2$ 且 $|\ell' \cap P| \ge 2$。

Output Format

你的程序需要向标准输出写入数据。输出恰好 $n-2$ 行。对于每个 $1 \le i \le n-2$，你输出的第 $i$ 行必须包含一个整数，表示关于 $n$ 个点的输入点集 $P$ 的 $(i-1)$-象限的数量。

3
0 0
1 2
-1 4

2

4
0 0
1 2
-1 4
-1 1

0
4

10
47 20
4 30
3 21
44 12
46 34
18 18
19 50
48 23
22 3
19 22

2
12
20
18
20
30
28
1