Description

在图绘制中，一棵有根（连通）树 $T = (V, E)$（具有 $n$ 个顶点）的线性排列是一种平面绘制方式：树的 $n$ 个顶点被放置于一条水平线（例如 $x$ 轴）上，而 $(n-1)$ 条边则绘制为连接其端点的半圆弧，位于该线上方，如图 1 所示。这样的线性排列 $\pi$ 将每个顶点映射到一个从 $1$ 到 $n$ 的不同整数，代表其沿 $x$ 轴的坐标。

:::align{center}

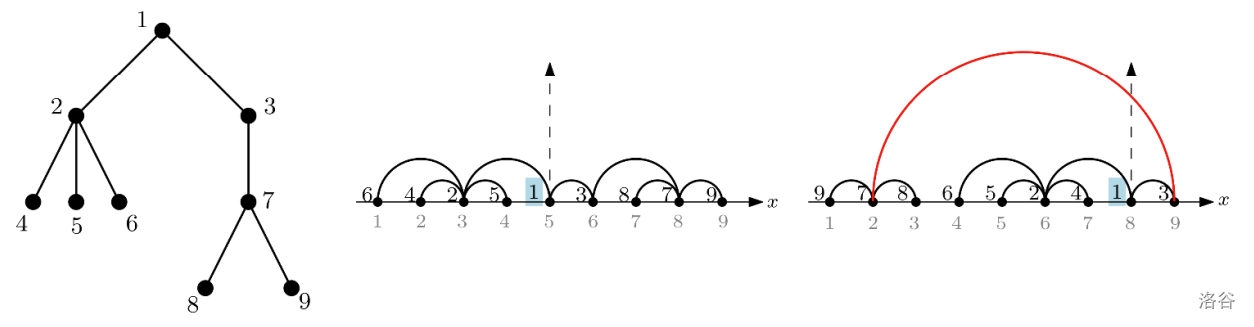
图 1. （左）一棵有九个顶点且以顶点 1 为根的有根树 $T$。
（中）$T$ 的一个洁净排列。
（右）$T$ 的一个不洁净排列，因为红色边 $(3,7)$ 覆盖了根。 :::

在一个线性排列 $\pi$ 中，两个顶点 $u$ 和 $v$ 之间的距离 $d(u, v)$ 定义为它们 $x$ 坐标之差的绝对值，即 $d(u, v) = |\pi(u) - \pi(v)|$。形式上，对于一棵有根树 $T = (V, E)$，其线性排列 $\pi$ 的代价定义为 $\sum_{(u,v) \in E} d(u, v)$。

一棵有根树 $T$ 的洁净排列 $\pi$ 是一种特殊的线性排列，它同时满足以下两个条件：

1. $\pi$ 中没有边交叉（除了共享端点的边之间）。
2. 没有边覆盖 $T$ 的根顶点 $r$，即不存在边 $(u, v)$ 使得 $\pi(u) < \pi(r) < \pi(v)$。

例如，图 1 中间是左边 $T$ 的一个洁净排列，但右边不洁净，因为边 $(3,7)$ 覆盖了根顶点 1。中间洁净排列的代价是 $11$，其中有三条距离为 $2$ 的边和五条距离为 $1$ 的边。这个代价是所有 $T$ 的洁净排列中最小的。

给定一棵以顶点 $1$ 为根的有根树，请编写一个程序，输出该树所有洁净排列中可能的最小代价。

Input Format

你的程序需要从标准输入读取数据。输入的第一行包含一个整数 $n$ ($2 \le n \le 5,000$)，其中 $n$ 是有根树的顶点数。顶点编号从 $1$ 到 $n$，根顶点是 $1$。接下来的 $(n-1)$ 行，每行包含两个正整数 $u$ 和 $v$，表示树的一条（无向）边 $(u, v)$ 的端点，其中 $u$ 和 $v$ 是 $1$ 到 $n$ 之间的不同整数。

Output Format

你的程序需要向标准输出写入数据。输出恰好一行。该行应包含以顶点 $1$ 为根的树的洁净排列的最小代价。

以下展示了两个测试用例的样例输入和输出。第二个测试用例对应图 1。

4
1 2
3 2
2 4

4

9
2 4
2 5
7 3
9 7
1 2
3 1
7 8
6 2

11

Hint

翻译由 DeepSeek V3 完成