Description

Jaehyun 喜欢数字。在 10 个数字中，6、7、8 和 9 是他的最爱。因此，他制作了一套只包含 6、7、8 和 9 的特殊卡牌。

目前，Jaehyun 拥有 $N \times M$ 张卡牌。他想要制作一个神奇的 $N$ 行 $M$ 列的卡牌矩阵。矩阵的每一行应包含 $M$ 张卡牌。他已经将自己的卡牌排列成一个 $N$ 行 $M$ 列的矩阵。

:::align{center}

图 1. 初始状态，不满足点对称。 :::

要成为一个神奇矩阵，该矩阵必须是点对称的：将矩阵旋转 180 度后得到的结果与原矩阵相同。例如，8 与自身点对称，而 6 和 9 相互点对称。 Jaehyun 不想改变卡牌的位置，因此他的目标是通过仅在原始位置上旋转卡牌来使矩阵点对称。

:::align{center}

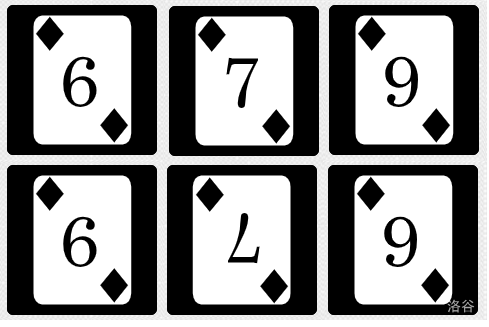
图 2. 旋转两张卡牌后，它们点对称。 :::

请找出使矩阵成为神奇矩阵所需旋转的最小卡牌数量。

Input Format

第一行包含两个整数 $N$ 和 $M$（$1 \le N, M \le 500$）。

接下来的 $N$ 行，每行包含一个由 $M$ 个字符组成的字符串，表示每张卡牌上写的数字。保证每个字符是 $\texttt{6}$、$\texttt{7}$、$\texttt{8}$ 或 $\texttt{9}$ 之一。

Output Format

第一行输出使矩阵成为神奇矩阵所需旋转的最小卡牌数量。如果无法制作神奇矩阵，则输出 $\texttt{-1}$（不带引号）。

2 3
676
679

2

3 3
888
888
888

0

1 1
7

-1

Hint

翻译由 DeepSeek V3 完成