Description

给定两个整数 $n$ 和 $m$，你需要构造一张有向无环图（DAG）$G = (V, E)$，其中包含恰好 $n$ 个顶点和 $m$ 条边。

在图 $G$ 中，如果从顶点 $u$ 出发存在一条路径到达顶点 $v$，则称顶点 $v$ 可达于顶点 $u$。

对于一个非空顶点集合 $A \subseteq V$，如果存在顶点 $w$ 能够从 $A$ 中的每一个顶点到达，则称 $w$ 对于集合 $A$ 是 良好 的。记 $f(A)$ 为对集合 $A$ 来说所有 良好 顶点组成的集合。

你构造的图必须满足以下两个条件：

• 对于每个顶点 $i$（$1 \leq i \leq n$），它都必须是从顶点 $1$ 可达 的。
• 存在 $k$ 个两两不同的非空顶点集合 $S_1, S_2, \ldots, S_k$，使得 $f(S_1), f(S_2), \ldots, f(S_k)$ 两两不同。注意，$f(S_i)$ 允许为空。

为了证明你构造的图 $G$ 满足上述第二条条件，你还需要输出这 $k$ 个集合 $S_1, S_2, \ldots, S_k$。

Input Format

输入仅一行，包含三个整数 $n, m, k$。

本题中仅有 $2$ 个测试数据：

• $n = 5$, $m = 6$, $k = 6$；
• $n = 100$, $m = 128$, $k = 16\,000$。

Output Format

输出前 $m$ 行描述你构造的图 $G$。每一行包含两个整数 $u, v$，表示图中的一条边，从 $u$ 指向 $v$。

接下来输出 $k$ 行，描述你给出的 $k$ 个顶点集合。第 $i$ 行首先输出集合 $S_i$ 的大小，然后输出该集合中的各个顶点。

5 6 6

1 2
1 3
2 4
3 5
2 5
3 4
1 1
1 2
1 3
1 4
1 5
2 2 3

Hint

在示例中，输出构造了一张有 $n = 5$ 个顶点、$m = 6$ 条边的图。对应的 $k = 6$ 个集合为：

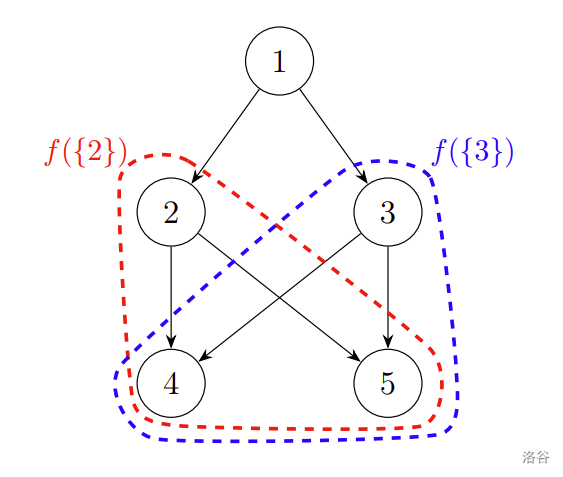
$S_1 = \{1\},\ S_2 = \{2\},\ S_3 = \{3\},\ S_4 = \{4\},\ S_5 = \{5\},\ S_6 = \{2, 3\}$。

其中，从 $S_6 = \{2, 3\}$ 的任一顶点出发，都可以到达顶点 $4$ 和 $5$，因此有 $f(\{2, 3\}) = \{4, 5\}$。

结合：

• $f(S_1) = \{1, 2, 3, 4, 5\}$
• $f(S_2) = \{2, 4, 5\}$
• $f(S_3) = \{3, 4, 5\}$
• $f(S_4) = \{4\}$
• $f(S_5) = \{5\}$
• $f(S_6) = \{4, 5\}$

可以看到这些集合两两不同，满足题目要求。

:::align{center} :::

翻译由 ChatGPT-5 完成