Description

以下故事基于真实事件——嗯，其中姓名已作修改，毕竟这类故事总是要改名字的。

Taylor Swift 教授正在批改一份关于整数斜堆（skiff heap）的作业。斜堆是一种二叉树，每个节点存储一个整数，且任意节点的值都小于或等于其所有子节点的值。注意斜堆不必是完全二叉树；也就是说，任意节点的左子树和（或）右子树可能为空。

将值 $x$ 插入斜堆 $H$ 的递归过程如下：

• 如果 $H$ 为空，则将 $H$ 变为仅包含一个值为 $x$ 的节点的斜堆。
• 否则，设 $y$ 为 $H$ 根节点的值。
  • 如果 $y < x$，则交换根节点的两个子树，并将 $x$ 递归插入新的左子树。
  • 如果 $y \ge x$，则创建一个值为 $x$ 的新节点，并将 $H$ 作为该新节点的左子树。

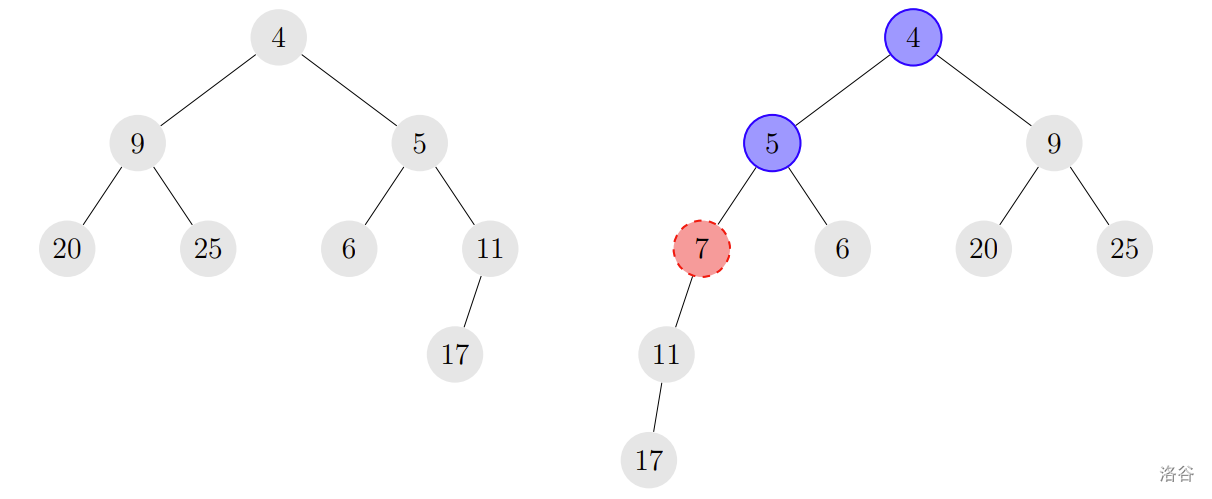
图 A.1：将值 $7$ 插入斜堆的示例。存储值 4 和 5 的节点（蓝色标记）交换了它们的子节点，而存储值 $11$ 的节点成为新插入节点（红色标记）的左子节点。

现在回到 Swift 教授的故事。她布置的作业要求学生展示将数字 $1$ 到 $n$ 的某个给定排列按给定顺序依次插入空堆后得到的堆结构。令人惊讶的是，有些学生的答案是错误的！这让 Swift 教授思考：对于一个给定的堆，是否存在一个输入排列能够生成这个堆？如果存在，字典序最小和最大的输入排列分别是什么？

Input Format

第一行输入包含一个整数 $n$（$1 \le n \le 2 \cdot 10^5$），表示树中的节点数。这些节点恰好包含从 $1$ 到 $n$ 的数字。

接下来是 $n$ 行，第 $i$ 行包含两个整数 $l_i$ 和 $r_i$（$i < l_i \le n$ 或 $l_i = 0$；$i < r_i \le n$ 或 $r_i = 0$），描述了存储值 $i$ 的节点的左孩子和右孩子的值，其中 $0$ 表示对应的孩子不存在。数据保证描述了一棵二叉树。

Output Format

输出在斜堆插入方法下能够产生给定树的字典序最小的输入排列，然后是字典序最大的输入排列。这两个排列可能相同，如果相同你仍然需要输出两者。如果不存在能够产生给定树的输入排列，输出 impossible。

7
2 3
4 5
6 7
0 0
0 0
0 0
0 0

1 3 2 7 5 6 4
7 1 5 3 2 6 4

2
0 2
0 0

impossible

3
2 0
3 0
0 0

2 3 1
3 2 1