Description

有一个连通无向简单仙人掌图$^{1}$，包含 $N \leq 1000$ 个节点和 $M$ 条边。节点带有颜色（用 $0$ 到 $1499$ 之间的非负整数表示）。最初所有节点的颜色均为 $0$。有一个确定性无记忆机器人$^{2}$在该图中探索，它通过在节点之间移动来完成探索任务。它必须至少访问所有节点一次，然后终止。

机器人从某个节点开始，这个节点可以是图中的任意节点。在每一步中，它能看到自己所在节点的颜色，以及所有相邻节点的颜色——相邻节点的顺序对于当前节点是固定的（即使重新访问节点时，相邻节点的颜色已经不同，机器人看到的顺序仍然保持不变）。机器人在每一步中必须执行以下两个动作之一：

1. 决定终止。
2. 为当前节点选择一个新的（或保持原样的）颜色，并选择要移动到的一个相邻节点。相邻节点用索引 $0$ 到 $D-1$ 标识，其中 $D$ 是相邻节点的数量。

在第二种情况下，当前节点会被重新染色（或保持原有颜色），然后机器人移动到所选的相邻节点。这个过程不断重复，直到机器人终止，或者达到迭代上限。若机器人能在 $L = 3000$ 步迭代内访问所有节点并终止，则视为胜利，否则失败。

你需要为机器人设计一个策略，使其能在任意这样的仙人掌图上完成任务。同时，你还需要尽量减少使用的不同颜色的数量。注意，颜色 $0$ 永远计入已使用的颜色。

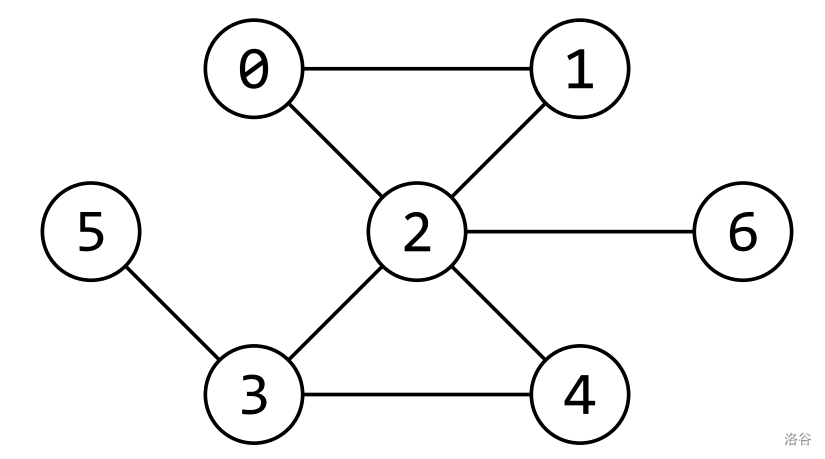
$^{1}$连通无向简单仙人掌图是一个连通无向简单图（任意节点间均可达，边是双向的，没有自环或重边），并且每条边至多属于一个简单环（简单环指每个节点最多出现一次的环）。下图是一个例子：

:::align{center} :::

$^{2}$若机器人的动作只依赖于当前输入（即不存储任何历史信息），并且在相同输入下总是做出相同动作，那么它是确定性无记忆机器人。

实现细节

机器人的策略应实现如下函数：

std::pair<int, int> navigate(int currColor, std::vector<int> adjColors)

• 参数为当前节点的颜色 currColor 和所有相邻节点的颜色（顺序固定）。
• 返回一个二元组：
  • 第一个元素表示当前节点的新颜色；
  • 第二个元素表示机器人要移动到的相邻节点索引。
• 如果机器人应终止，则返回 $(-1, -1)$。

该函数会被反复调用以决定机器人的动作。由于它是确定性的，如果 navigate 已经在某些参数下被调用过，则不会再用相同参数调用，而是直接复用上一次的返回值。此外，每个测试最多包含 $T \leq 5$ 个子测试（不同的图或起始点），这些子测试可能并发运行（即你的程序可能会交替收到不同子测试的调用）。最后，navigate 的调用可能发生在不同的程序执行中（也可能有时发生在同一次执行中）。你的程序总共会被执行 $P = 100$ 次。因此，程序不应尝试在不同调用之间传递信息。

Hint

示例

考虑题面图示中的样例图，有 $N = 7$ 个节点，$M = 8$ 条边：$(0,1)$，$(1,2)$，$(2,0)$，$(2,3)$，$(3,4)$，$(4,2)$，$(3,5)$，$(2,6)$。此外，由于相邻节点顺序与节点的邻接表顺序相关，我们在下表中给出：

假设机器人从节点 5 开始，则可能出现如下（失败的）交互过程：

此过程中机器人使用了 6 种不同颜色：$0,1,2,3,4,8$（注意即使机器人从未返回颜色 $0$，由于所有节点初始颜色为 $0$，它仍计入使用的颜色）。机器人共执行 9 次迭代后终止，但失败了，因为它在终止时尚未访问节点 1。

$^{1}$注意第 4 步的调用实际上不会发生，因为它与第 1 步的调用参数完全相同，测评器会直接复用第 1 步的返回值。但它仍然计入机器人迭代次数。

样例测评器

样例测评器不会多次执行你的程序，因此所有对 navigate 的调用都会发生在同一次程序执行中。

输入格式如下：首先读入 $T$（子测试数量）。然后对每个子测试：

• 第 1 行：三个整数 $N, M, S$（图的节点数、边数、机器人起始节点）。
• 接下来 $M$ 行：每行两个整数 $A_i, B_i$，表示边 $i$ 连接的两个节点（$0 \leq A_i, B_i < N$）。

样例测评器会打印出你的解使用的不同颜色数量，以及终止前的迭代次数。若解失败，会打印错误信息。

默认情况下，样例测评器会输出机器人每步看到的状态和执行的动作。你可以通过将 DEBUG 从 true 改为 false 来关闭此功能。

约束条件

• $3 \leq N \leq 1000$
• $0 \leq \text{Color} < 1500$
• $L = 3000$
• $T \leq 5$
• $P = 100$

评分规则

在某个子任务中，你获得的分数比例 $S$ 取决于 $C$ —— 你的解在该子任务及其所有依赖子任务中使用的最大不同颜色数量（包括颜色 0）：

• 若你的解在任一子测试失败，则 $S = 0$；
• 若 $C \leq 4$，则 $S = 1.0$；
• 若 $4 < C \leq 8$，则 $S = 1.0 - 0.6 \dfrac{C - 4}{4}$；
• 若 $8 < C \leq 21$，则 $S = 0.4 \dfrac{8}{C}$；
• 若 $C > 21$，则 $S = 0.15$。

子任务

$^{1}$环图的边为：$(i, (i+1) \bmod N)$，其中 $0 \leq i < N$。

$^{2}$星图的边为：$(0,i)$，其中 $1 \leq i < N$。

$^{3}$链图的边为：$(i, i+1)$，其中 $0 \leq i < N-1$。

$^{4}$树是没有环的图。

翻译由 ChatGPT-5 完成。