Description

两个经典的图算法——深度优先搜索和广度优先搜索——在图中分别构造出两棵生成树。深度优先搜索生成的树没有“水平”边，即连接两个互为非祖先关系顶点的边；而广度优先搜索生成的树没有“垂直”边，即连接某个顶点与其祖先的边。在本题中，你需要构造一棵具有指定数量水平边和垂直边的中间生成树。

回顾一下，无向图由顶点集 $V$ 和边集 $E$ 组成，每条边连接两个顶点。我们只考虑连通图，即任意两个顶点之间都可以通过边到达。树是一个连通且无环的无向图，图中的生成树是其边的一个子集，能够构成一棵树，使得任意两个顶点之间都可以互达。树有两个基本性质：一棵有 $n$ 个顶点的树恰好有 $n-1$ 条边，并且任意两点之间有且仅有一条简单路径。

我们指定图中的一个顶点 $r$ 作为树的“根”。在从顶点 $x$ 到根 $r$ 的唯一路径上的所有顶点，称为 $x$ 的“祖先”；路径上的第一个顶点称为 $x$ 的“父亲”，记作 $p_x$。根没有父亲。

如果在图中固定了根和生成树，则所有边可以分为三类：

• “树边”——所选生成树中的边；
• “垂直边”——不属于树的边，连接某个顶点与其祖先；
• “水平边”——其余的边。

:::align{center} :::

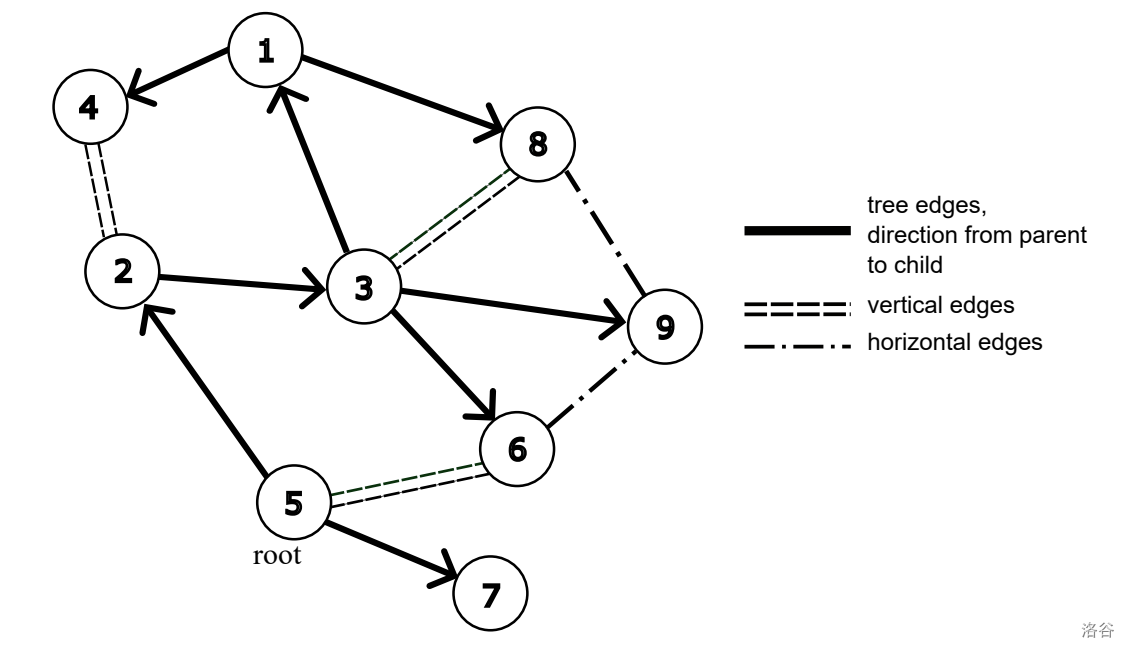生成树的“垂直度”定义为图中垂直边的数量。

给定一个有 $n$ 个顶点和 $m$ 条边的图，树的根 $r$，以及一个整数 $h$，$0 \le h \le m-n+1$。你需要构造一棵以 $r$ 为根、垂直度为 $h$ 的生成树，或者报告不存在这样的树。

Input Format

每组测试数据包含若干组输入。第一行包含一个整数 $t$，表示测试数据组数（$1 \le t \le 10^5$）。接下来是 $t$ 组测试数据的描述。

每组测试数据的第一行包含四个整数 $n$、$m$、$r$ 和 $h$，分别表示图的顶点数、边数、根的编号和所需生成树的垂直度（$2 \le n \le 3 \cdot 10^5$；$n-1 \le m \le 3 \cdot 10^5$；$1 \le r \le n$；$0 \le h \le m-n+1$）。

接下来的 $m$ 行，每行包含两个整数 $u_i$、$v_i$，表示一条连接顶点 $u_i$ 和 $v_i$ 的边（$1 \le u_i, v_i \le n$；$u_i \ne v_i$）。

保证所有图都是连通的，没有自环和重边。保证所有测试数据中 $n$ 的总和不超过 $3 \cdot 10^5$，$m$ 的总和不超过 $3 \cdot 10^5$。

Output Format

对于每组测试数据，找到所需的生成树 $T$，并在单独一行输出 $n$ 个整数 $p_1, p_2, \ldots, p_n$，其中 $p_i$ 表示第 $i$ 个顶点在树 $T$ 中的父亲编号（$1 \le p_i \le n$）。对于 $p_r$，你可以输出 $1$ 到 $n$ 之间的任意数。如果不存在满足条件的树 $T$，则输出 $n$ 个 $-1$。

4
5 7 2 0
1 2
2 3
3 4
4 1
3 5
5 4
1 5
5 7 2 1
1 2
2 3
3 4
4 1
3 5
5 4
1 5
5 7 2 2
1 2
2 3
3 4
4 1
3 5
5 4
1 5
5 7 2 3
1 2
2 3
3 4
4 1
3 5
5 4
1 5

2 1 2 3 3
2 1 4 1 1
2 1 5 5 1
2 1 4 1 3

Hint

由 ChatGPT 4.1 翻译