Description

物理可以非常有趣！ 昨天，你的老师讲解了干涉现象的原理：如果你有两列波，它们在整个波长范围内的高度会相加！ 因此，如果两列波都在波峰处，合成后的波峰会更高。 同样地，如果两列波都在水面以下的波谷处，合成后的波谷会更低。 从技术上讲，波的高度被称为振幅，两波峰之间的距离被称为波长。

:::align{center}

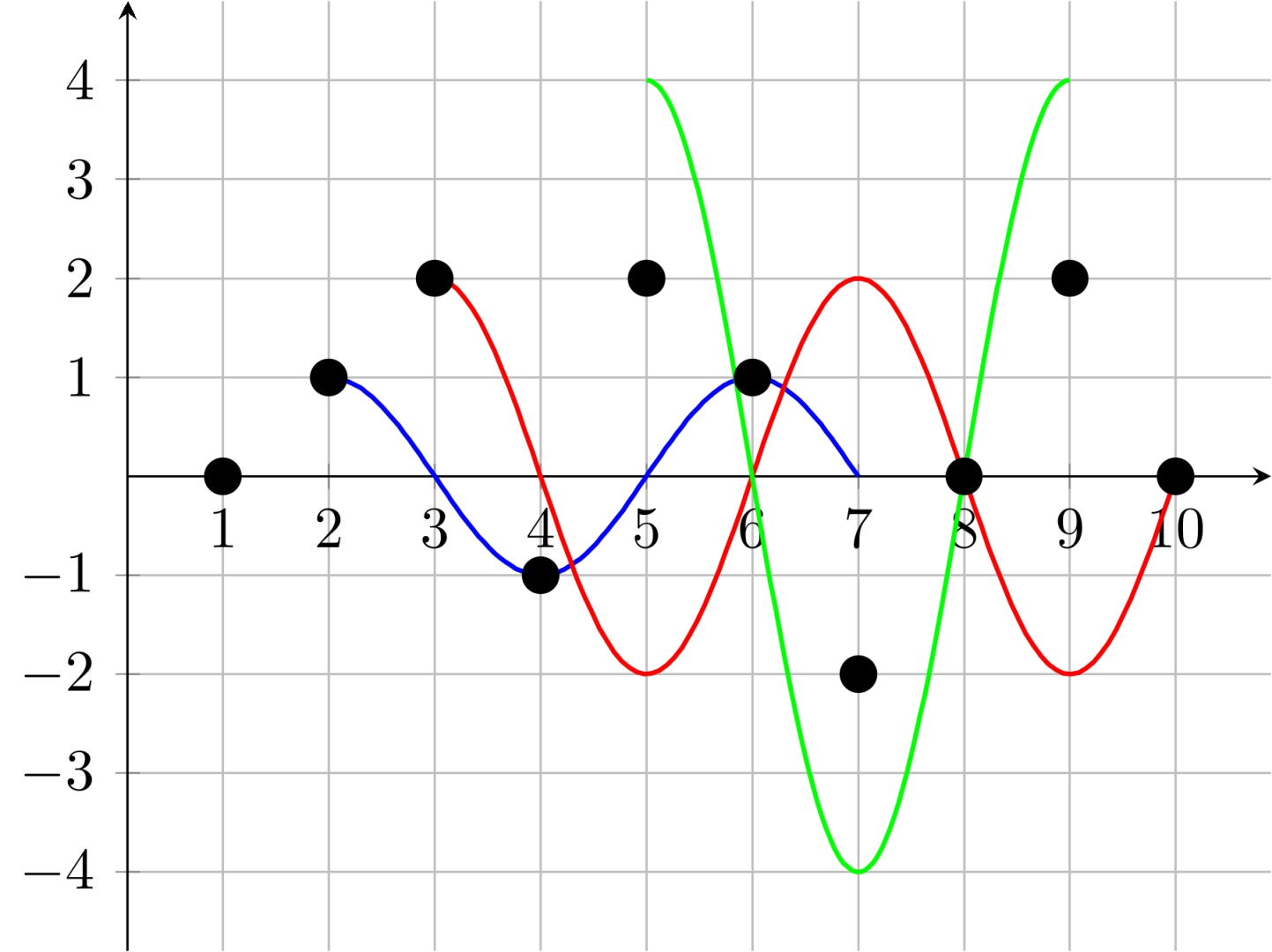
图 I.1：样例输入 2 中三列波的干涉效果。黑点表示合成波在各点的高度。 :::

今天，你的物理老师描述了她即将进行的一个实验的设置。 她将在一维水槽中制造驻波。 由于她对物理元素的精确控制，所有波都具有精确控制的振幅，并且只会在给定长度的区间内产生。 每列波的波长始终为 $4$，且第一个正波峰总是在区间的第一个位置。 我们只在整数点上测量波的振幅。 例如，振幅为 $2$，长度为 $9$ 的一列波可以表示为 $\texttt{2\ 0\ -2\ 0\ 2\ 0\ -2\ 0\ 2}$。 如果某个点没有波，则振幅为 $0$。 你的任务是预测在给定位置处，考虑到之前所有产生的波后，合成波的高度。

Input Format

输入包含：

• 一行两个整数 $n$ 和 $w$（$1 \le n \le 4000$，$1 \le w \le 10^9$），分别表示操作数和水槽的宽度。
• 接下来 $n$ 行，每行是波的描述或预测任务：
  • “$\texttt{!}\ p\ \ell\ a$”，表示一列波的描述，起始位置为 $p$，长度为 $\ell$（$1 \le p, \ell \le w$），振幅为 $a$（$1 \le a \le 10^9$）。保证 $p+\ell-1 \le w$。
  • “$\texttt{?}\ p$”，表示对位置 $p$（$1 \le p \le w$）的预测任务。

参见图 I.1 以部分可视化样例 2。

Output Format

对于每个预测任务，输出一行一个整数，表示在所询问位置处，所有已描述波的合成波的高度。

4 10
! 2 7 1
? 9
? 7
? 6

0
0
1

7 10
! 2 6 1
! 3 8 2
! 5 2 3
? 6
! 5 5 4
? 8
? 9

1
0
2

6 12
! 1 7 1
! 7 3 2
? 6
? 7
? 8
? 10

0
1
0
0

6 11
! 1 6 1
? 6
! 5 7 4
? 6
! 6 3 2
? 6

0
0
2

Hint

由 ChatGPT 4.1 翻译