Description

当不在思考这些抽象哲学问题时，忒修斯会在闲暇时猎杀弥诺陶洛斯。但这一次，他必须先穿过一个黑暗而扭曲的迷宫。由于这并非易事，他请求阿里阿德涅为他引路。这个迷宫可以看作是一个连通的无向图，包含 $n$ 个节点（编号 $1$ 到 $n$）和 $m$ 条边，并且有一个特殊节点 $t$，弥诺陶洛斯就在这里。

忒修斯完全看不到图的全貌，但阿里阿德涅可以。两人会先商定一个策略，使他能安全到达弥诺陶洛斯所在的节点：阿里阿德涅会在 $m$ 条边的每一条上贴上 $0$ 或 $1$ 的标签。之后，忒修斯会从某个节点 $s$ 进入迷宫，而阿里阿德涅事先并不知道 $s$ 的位置。

由于迷宫极为黑暗，任何时刻他只能看到当前所在节点的编号、相邻节点的编号以及相邻边的标签。此外，由于迷宫结构扭曲，他永远无法记住自己之前到过的节点的任何信息。

为了安全到达弥诺陶洛斯，忒修斯必须在不超过 $\min + C$ 次移动内完成，其中 $\min$ 是从 $s$ 到 $t$ 的最短路径上的边数，$C$ 是一个常数。

实现细节

你需要实现两个函数：

std::vector<int> label(int n, std::vector<std::pair<int,int>> edges, int t);

• $n$：图的节点数
• $edges$：长度为 $m$ 的数组，描述图的边
• $t$：目的节点
• 该函数应返回一个长度为 $m$ 的标签数组，第 $i$ 个元素只能是 $0$ 或 $1$，表示第 $i$ 条边的标签（$0 \leq i < m$）。
• 每条边必须贴上 $0$ 或 $1$，使用其他标签会导致未定义行为。
• 每个测试用例中，该函数恰好调用一次。

int travel(int n, int u, std::vector<std::pair<int,int>> neighbours);

• $n$：图的节点数
• $u$：当前所在节点
• $neighbours$：由若干对 $(v, e)$ 组成的列表，表示 $u$ 与节点 $v$ 之间有一条标签为 $e$ 的边
• 该函数应返回一个相邻节点的编号，表示下一步要移动到的节点。如果返回的节点是 $t$，程序会自动终止。
• 保证该函数被调用时，$u$ 不会等于特殊节点 $t$。
• 每次调用该函数代表在迷宫中移动一次，因此对于每个测试用例，该函数可以被调用任意多次，直到到达终点。

注意！ 程序不能使用全局或静态变量在不同的 label 或 travel 调用之间传递信息。任何试图绕过这一限制的行为都会导致未定义行为。

Hint

示例 1

假设我们有一个包含 $7$ 个节点和 $7$ 条边的图（如下所示）。起点 $s$ 为节点 $3$（绿色标记），终点 $t$ 为节点 $7$（红色标记）。评测程序会首先调用：

label(7, {{1, 6}, {7, 6}, {2, 5}, {3, 2}, {3, 6}, {6, 5}, {6, 4}}, 7)

假设 label 返回 {0, 1, 1, 1, 0, 1, 0}，则图形如下：

:::align{center} :::

接下来可能的 travel 调用过程如下（能得到正确结果）：

当返回值为 $7$（即到达目的地）时，程序终止。

数据范围

• $1 \leq n \leq 10000$
• $1 \leq m \leq 50000$
• $C = 14$
• 在调用 label 前，起点 $s$ 对于该测试用例是固定的。

子任务

1. （4 分）图是一个完全图（即 $1 \leq u < v \leq n$ 间都有一条边）
2. （10 分）从终点到任意节点的距离至多为 $2$ 条边
3. （11 分）图是一棵树
4. （13 分）图是二分图（即可以将节点分为两个集合，同一集合内没有边）
5. （12 分）图是梯形图（定义见下）
6. （50 分）无额外限制

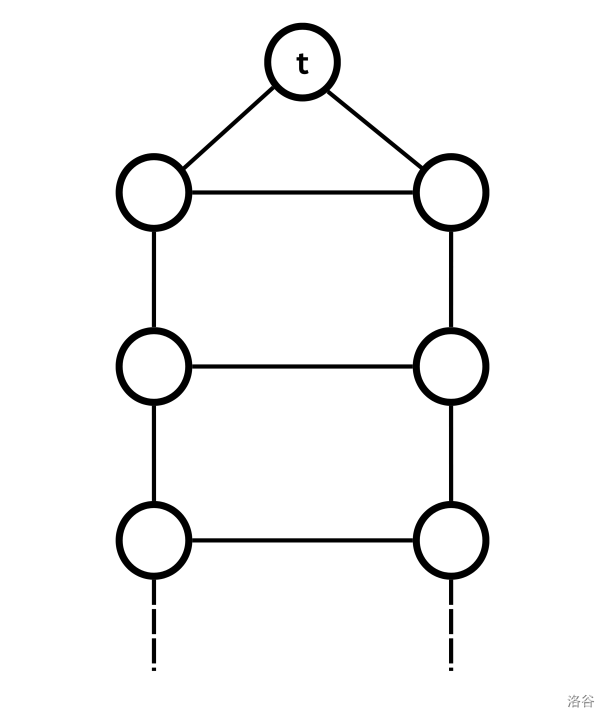
注： 梯形图由两条长度相等的平行路径（链）组成，对应位置的节点间用边相连形成梯子横档。在梯子一端有一个特殊节点——终点 $t$，它连接到两条路径的两个端点，相当于一个公共父节点。保证这种图中 $n$ 为奇数。见下图：

:::align{center} :::

翻译由 ChatGPT-5 完成