Description

最近，生物学家 Ina 在池塘的睡莲叶上发现了一种新的青蛙物种。她观察这些青蛙一段时间后发现，它们非常注重个人空间，总是避免与其他青蛙共用同一片睡莲叶。此外，它们似乎很懒惰，很少移动，即使移动，也总是跳到最近的空睡莲叶上。

:::align{center}

池塘中的一只青蛙。 :::

为了验证她关于青蛙移动模式的假设，Ina 在实验室的池中布置了大量睡莲叶，并将它们排成一条直线。由于青蛙会被光吸引，她进一步简化了实验装置，在直线的一端放置了一盏明亮的灯。这样，青蛙总是朝着光的方向跳跃（即只会向编号更大的方向跳）。

当然，Ina 现在可以把一些青蛙放到睡莲叶上，然后整天坐在那里观察青蛙跳跃。但由于青蛙很少移动，收集足够的数据将耗费大量时间。

因此，她在每只青蛙身上安装了一个微型装置，可以记录该青蛙的所有跳跃。这样，她就可以把青蛙放到睡莲叶上，离开几个小时后再回来收集数据。不幸的是，这些装置必须非常小，没有空间安装定位系统；它们只能记录每次跳跃的时间。

但如果青蛙的移动模式像 Ina 所想的那样受限，仅凭初始位置和记录的跳跃时间戳，是否一定可以还原每只青蛙的具体移动轨迹呢？

Input Format

输入包括：

• 一行一个整数 $n$（$1\leq n \leq 2\cdot10^5$），表示青蛙的数量。
• 一行 $n$ 个整数 $x_1,\dots, x_n$（$1\leq x_i \leq 10^6$），表示第 $i$ 只青蛙最初所在的睡莲叶编号。睡莲叶的编号从 $1$ 开始，连续递增。保证初始位置严格递增，即 $x_1 < x_2 < \dots < x_n$。
• 一行一个整数 $q$（$1\leq q \leq 2\cdot10^5$），表示记录到的跳跃次数。
• 接下来 $q$ 行，每行一个整数 $i$（$1\leq i\leq n$），表示第 $i$ 只青蛙跳跃了一次。跳跃按时间顺序给出，可以假设一只青蛙落地后，下一次跳跃才会开始。青蛙总是跳到编号更大的最近的空睡莲叶，并且可以假设总能找到这样的睡莲叶。

Output Format

对于每一次跳跃，输出青蛙落下的睡莲叶编号。

5
1 2 3 5 7
3
1
2
4

4
6
8

5
1 2 3 5 7
4
1
1
1
1

4
6
8
9

Hint

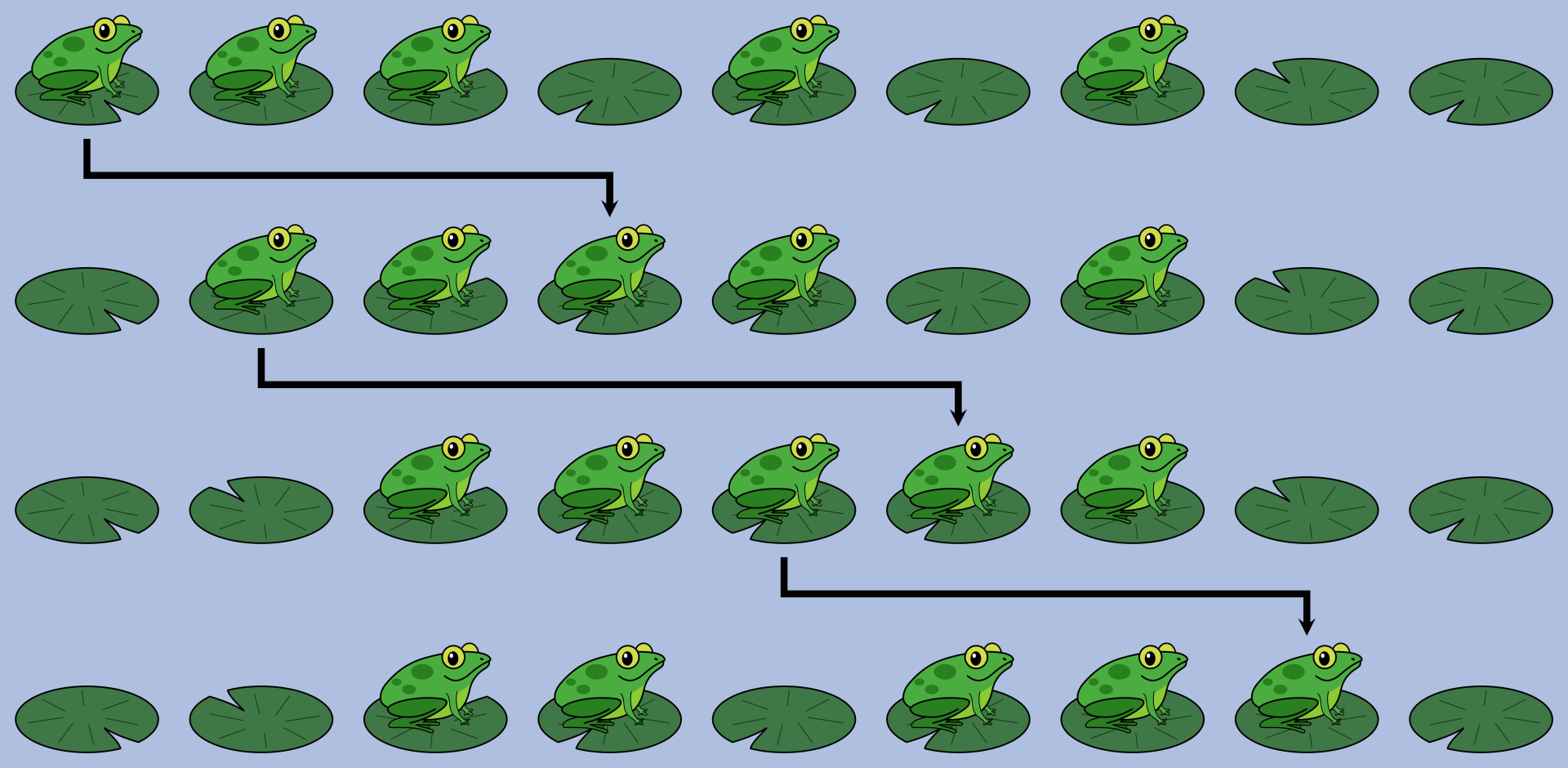
:::align{center} 图 I.1：第一个样例的示意图。睡莲叶从左到右编号，从 $1$ 开始。 :::

由 ChatGPT 4.1 翻译