Description

给定四个整数 $A$、$B$、$C$、$D$，满足 $A < B < C < D$。我们将它们以某种顺序放在正方形的四个角上，并画出一个环 $A - B - C - D - A$。根据整数的排列方式，我们可以得到不同形状的环，但有些排列会产生相同的形状：

我们可以得到三种不同的环形状：

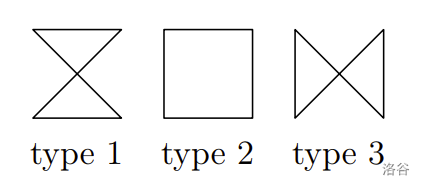
现在，考虑一个 $n\times m$ 的矩阵，矩阵中填有 $1$ 到 $nm$ 的互不相同的整数。矩阵中的每一个 $2\times 2$ 的小方格都可以看作是一个四角有整数的正方形。我们像上面一样，为每个这样的正方形建立一个环：

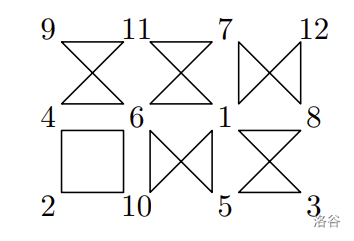
你的任务是进行逆操作。给定所有 $(n-1)(m-1)$ 个环的形状类型，请你构造一个 $n\times m$ 的矩阵，矩阵中填有 $1$ 到 $nm$ 的互不相同的整数，使得这些 $2\times 2$ 小方格对应的环形状与输入一致。

Input Format

第一行包含两个整数 $n$ 和 $m$，满足 $2\le n, m\le 500$。

接下来的 $n-1$ 行，每行包含一个长度为 $m-1$ 的字符串，中间没有空格。每个字符是 $1$ 到 $3$ 之间的数字，表示对应环的形状类型。

Output Format

输出一个 $n\times m$ 的矩阵，矩阵中填有 $1$ 到 $nm$ 的互不相同的整数，使得所有 $2\times 2$ 小方格对应的环形状与输入一致。

可以证明一定存在解。如果有多组解，输出任意一组均可。

3 4
113
231

9 11 7 12
4 6 1 8
2 10 5 3

Hint

由 ChatGPT 4.1 翻译