Description

这是一个交互题。

给定 $n$ 个平面上的点 $A_i = (x_i, y_i)$。已知所有 $x_i$ 互不相同，所有 $y_i$ 也互不相同。

你的任务是将这 $n$ 个点连接成一条折线。

折线由一个 $1$ 到 $n$ 的排列 $p_1, p_2, \ldots, p_n$ 决定。折线由 $n-1$ 条线段组成，第 $1$ 条线段连接 $A_{p_1}$ 和 $A_{p_2}$，第 $2$ 条线段连接 $A_{p_2}$ 和 $A_{p_3}$，依此类推，最后一条线段连接 $A_{p_{n-1}}$ 和 $A_{p_n}$。注意，线段之间可以相交。

折线的锐度（sharpness）定义为满足 $2 \leq i \leq n-1$ 且 $\angle A_{p_{i-1}} A_{p_i} A_{p_{i+1}}$ 为锐角（即严格小于 $90^\circ$）的 $i$ 的数量。

你需要解决以下四个任务：

• 求一条锐度最大的折线（即锐度尽可能大）。
• 给定整数 $c$，求一条锐度不超过 $c$ 的折线。
• 给定整数 $c$，
  有 $q$ 个询问，每次给定一个整数 $k_i$（$c \leq k_i \leq n-c$）。对于第 $i$ 个询问，你需要构造一条锐度恰好为 $k_i$ 的折线。
• 给定整数 $c$，
  对于每个 $k$ 从 $c$ 到 $n-c$，都要构造一条锐度恰好为 $k$ 的折线 $p^{(k)}$，并输出 $n-2c+1$ 个数 $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$，其中

$$\text{hash}(p) = \left( \sum\limits_{i=1}^n p_i b^{i-1} \right) \bmod m$$

这是排列 $p$ 的多项式哈希，参数 $b = 10^6 + 3$，$m = 10^9 + 7$。
然后有 $q$ 个询问，每次给定一个整数 $k_i$（$c \leq k_i \leq n-c$），你需要输出锐度恰好为 $k_i$ 的折线 $p^{(k_i)}$。会检查该折线的锐度是否为 $k_i$ 且哈希值是否等于之前输出的 $\text{hash}(p^{(k_i)})$。
注意这些询问会在你输出哈希值后出现。

保证在给定约束下，总有解存在。

交互协议

第一行输入两个整数 $\text{task}$、$\text{group}$（$1 \leq \text{task} \leq 4$，$0 \leq \text{group} \leq 21$），表示本次测试要解决的任务编号和测试组编号。

第二行输入一个整数 $n$（$3 \leq n \leq 80\,000$），表示点的数量。

接下来 $n$ 行，每行两个整数 $x_i, y_i$（$|x_i|, |y_i| \leq 10^9$），表示一个点的坐标。保证所有 $x_i$ 互不相同，所有 $y_i$ 互不相同。

若 $\text{task} = 1$，输入到此结束，你需要输出一组锐度最大的排列。交互结束。

若 $\text{task} \neq 1$，则下一行输入一个整数 $c$（$2 \leq c \leq \frac{n}{2}$）。

若 $\text{task} = 2$，输入到此结束，你需要输出一组锐度不超过 $c$ 的排列。交互结束。

若 $\text{task} = 4$，你需要输出 $n-2c+1$ 个整数 $\text{hash}\left(p^{(c)}\right), \text{hash}\left(p^{(c+1)}\right), \ldots, \text{hash}\left(p^{(n-c)}\right)$，其中 $0 \leq \text{hash}\left(p^{(i)}\right) < 10^9 + 7$。注意如果 $\text{task} = 3$，则不需要输出哈希。

只有当 $\text{task} = 3$ 或 $\text{task} = 4$ 时，才会有进一步交互。

下一行输入一个整数 $q$（$1 \leq q \leq 50$），表示询问数量。

接下来 $q$ 行，每行一个整数 $k_i$（$c \leq k_i \leq n-c$）。对于每次询问，你需要在一行输出一个排列，要求该排列的锐度恰好为 $k_i$。若 $\text{task} = 4$，还需保证该排列的哈希值与之前输出的 $\text{hash}(p^{(k_i)})$ 相同。

本题为交互题，每输出一行后不要忘记输出换行并刷新输出缓冲区。

1 0
4
2 3
1 8
4 2
0 0

3 2 4 1

2 0
5
-2 0
-1 -1
0 1
2 -2
3 -3
2

5 4 3 1 2

3 0
6
0 0
1 1
2 2
3 -3
4 -2
5 -1
2
3
2

3

4

1 2 3 4 5 6

4 5 6 1 3 2

6 2 4 3 5 1

4 0
5
-2 -1
-1 1
1 6
0 -3
2 0
2

2
2

3

534735187 776162084


4 5 1 2 3

1 3 2 5 4

Hint

说明

所有图中，锐角用双圆弧表示，非锐角用单圆弧表示。

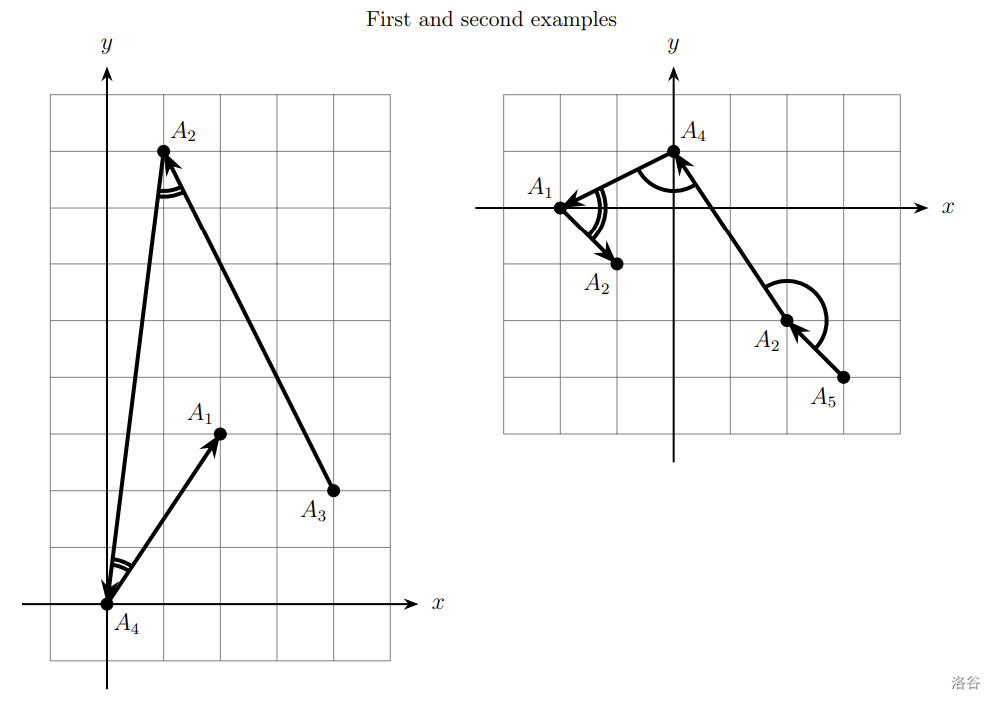
在第一个样例中，所有角都是锐角，因此折线的最大锐度为 $2$。

在第二个样例中，锐度为 $1$，满足 $\leq 2$。

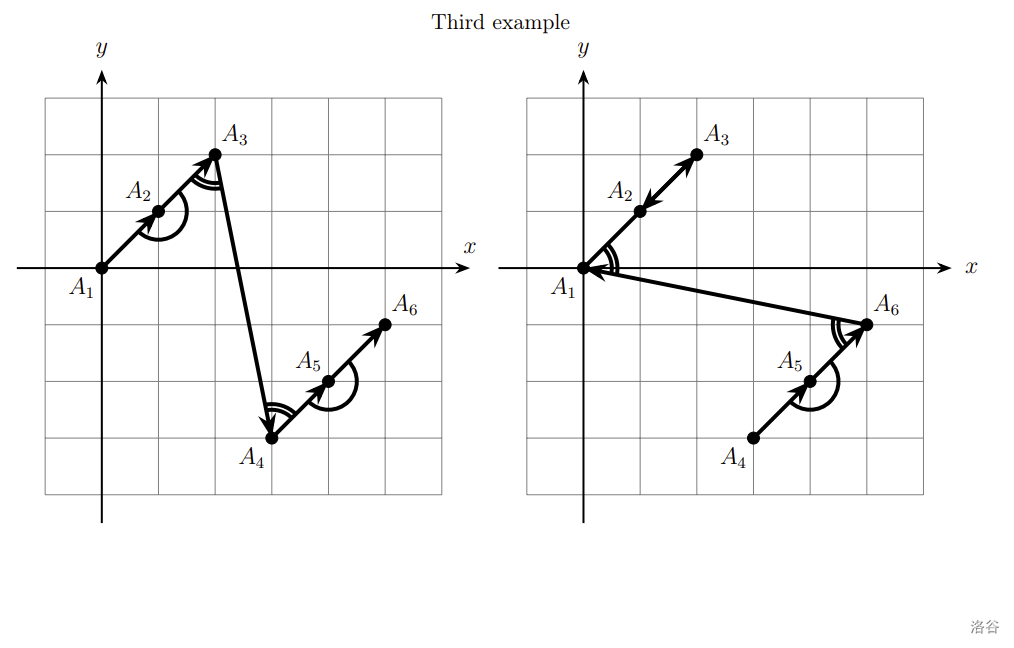
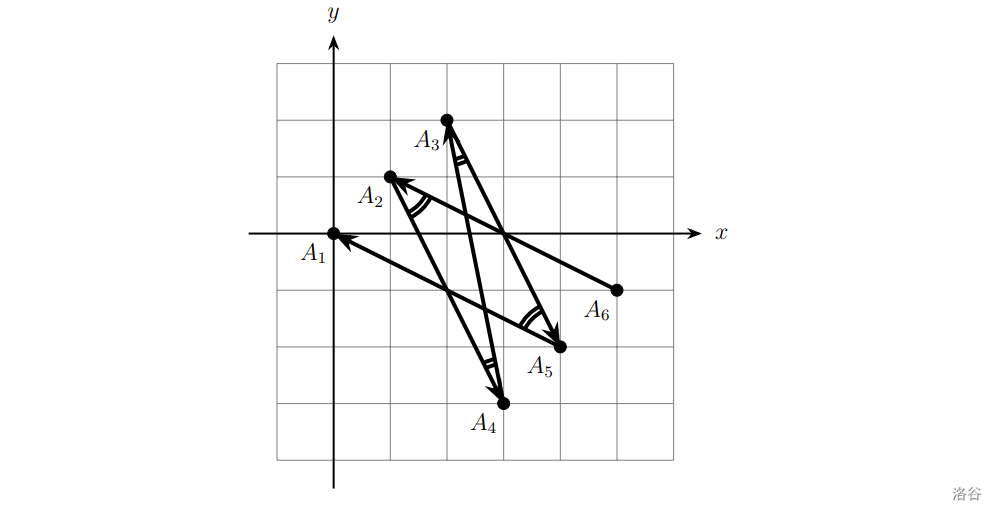
在第三个样例中，折线的锐度分别为 $2$、$3$、$4$。

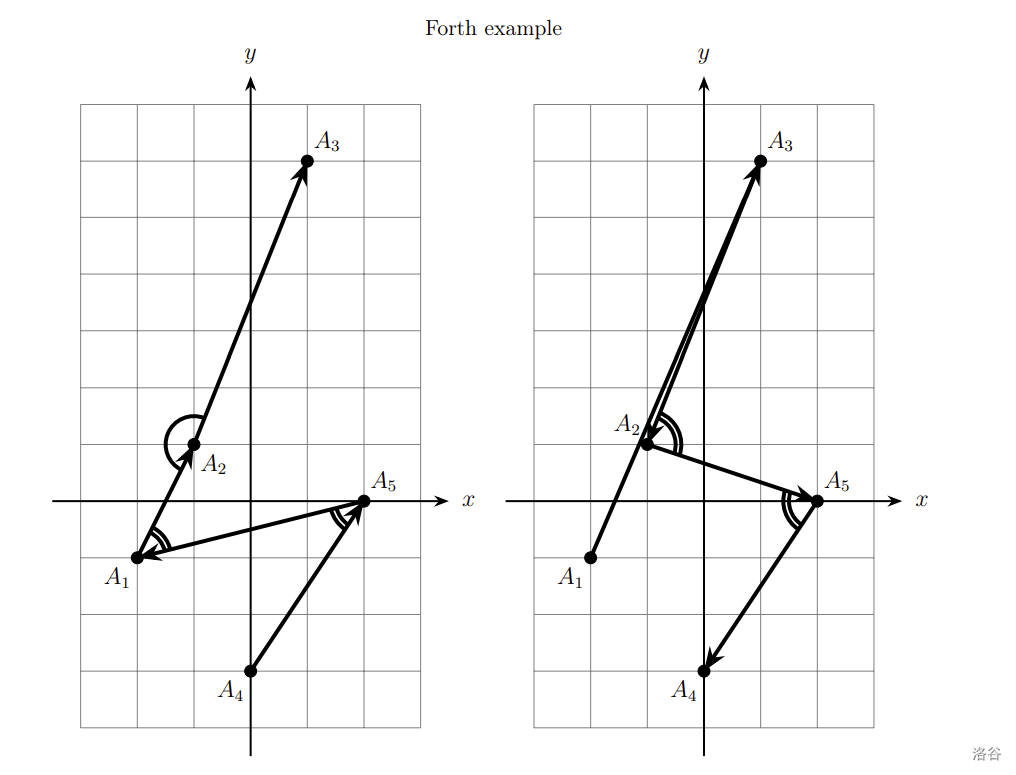
在第四个样例中，分别构造了锐度为 $2$ 和 $3$ 的折线，哈希值与之前输出的相同。

计分方式

本题共二十一组测试。只有通过该组及其所有依赖组的所有测试，才能获得该组的分数。

组别	分值	task	$n$	$c$	额外约束	依赖组	备注
0		-		-	-	-	样例。
1	8	1	$n \leq 20000$		$x_i < x_{i+1}, y_i < y_{i+1}$
2	6		$n \leq 10$		随机点
3	5		$n \leq 1000$			2
4			$n \leq 20000$			2 - 3
5	6				-	1 - 4
6	17	2	$n = 80000$	$c = 800$		-
7		3			$x_i < x_{i+1}, y_i < y_{i+1}$
8	4		$n = 50$	$c = 25$	随机点
9			$n = 200$	$c = 80$
10			$n = 1000$	$c = 300$
11	3		$n = 5000$	$c = 600$
12			$n = 80000$	$c = 35000$
13				$c = 5000$		12
14				$c = 2000$	-	12 - 13
15	2			$c = 800$		7, 12 - 14
16	6	4			$x_i < x_{i+1}, y_i < y_{i+1}$	-
17	3		$n = 5000$	$c = 600$	随机点
18			$n = 80000$	$c = 35000$
19				$c = 5000$		18
20				$c = 2000$	-	18 - 19
21	2			$c = 800$		16, 18 - 20

在说明为“随机点”的组别中，所有点的坐标 $x_i, y_i$ 均等概率随机生成于区间 $[-10^9, 10^9]$。

翻译由 ChatGPT-4.1 完成。