Description

Polygonovich 教授是 Flatland 的一位诚实市民，他喜欢在平面上的整数点之间进行随机行走。他每天早晨从原点出发，面朝北方。他有三种行动方式：

• 'F'：向前移动一个单位长度。
• 'L'：向左转 $90$ 度。
• 'R'：向右转 $90$ 度。

一天结束时（是的，他走了很久！），他会回到原点。他在行走过程中，除了原点外，绝不会两次经过同一个点，因此他的路径围成了一个多边形。下图中，多边形的内部被涂成了蓝色（暂时忽略 $x$、$y$、$z$ 和 $w$ 这几个点，稍后会解释）：

注意，只要 Polygonovich 教授转弯次数超过 $4$ 次，这个多边形就不是凸多边形，因此会出现“口袋”区域。

注意！ 为了增加难度，我们对“口袋”的定义可能与你以往听说的不同。

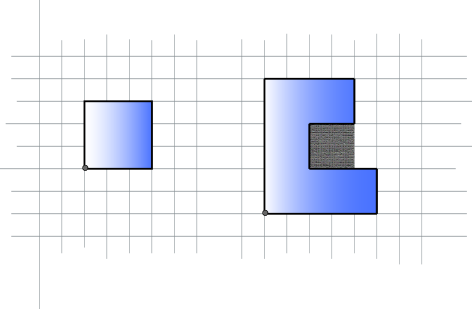
下图中灰色区域表示多边形的口袋。

形式化地说，一个点 $p$ 被认为在口袋中，当且仅当它不在多边形内部，并且满足以下两个条件之一：

• $p$ 的正东和正西方向上都存在边界点；或者
• $p$ 的正北和正南方向上都存在边界点。

边界点指的是 Polygonovich 先生在行走过程中经过的所有点（包括所有点，不仅限于整数坐标点）。

再看上面的第一张图。点 $x$ 满足第一个条件；$y$ 同时满足两个条件；$z$ 满足第二个条件。这三个点都在口袋中。点 $w$ 不在口袋中。

给定 Polygonovich 教授的行走路径，请你计算所有口袋区域的总面积。

Input Format

输入的第一行是测试用例数 $N$。接下来有 $N$ 组测试数据。

每组测试数据描述了 Polygonovich 教授的一次行走。每组数据以一个整数 $L$ 开头。接下来是 $L$ 个 "S T" 对，其中 $S$ 是仅由 'L'、'R'、'F' 组成的字符串，$T$ 是一个整数，表示 $S$ 重复的次数。

换句话说，每组测试数据的输入格式如下： $S_1$ $T_1$ $S_2$ $T_2$ ... $S_L$ $T_L$

实际的行动序列是 $T_1$ 个 $S_1$，接着 $T_2$ 个 $S_2$，依此类推，拼接而成。

同一组测试数据中的 "S T" 对可能不会全部在同一行，但字符串 $S$ 不会被拆分到多行。下面的第二个样例演示了这一点。

Output Format

对于每组测试数据，输出一行，格式为 "Case #$X$: $Y$"，其中 $X$ 是测试用例编号（从 $1$ 开始），$Y$ 是所有口袋区域的总面积。

2
1
FFFR 4
9
F 6 R 1 F 4 RFF 2 LFF 1
LFFFR 1 F 2 R 1 F 5

Case #1: 0
Case #2: 4

Hint

样例解释

下图展示了两个样例测试数据的情况。

数据范围

• $1 \leqslant N \leqslant 100$
• $1 \leqslant T$（上界见下述“小数据集”和“大数据集”说明）
• 输入拼接后的路径中不会出现连续的方向变化（即不会有 'LL'、'RR'、'LR' 或 'RL'），并且路径中至少包含一个 'F'。
• 路径不会自交，除了起点和终点重合，并且最终会回到原点。

小数据集（5 分，测试点 1 - 可见）

• $1 \leqslant L \leqslant 100$
• 每个字符串 $S$ 的长度为 $1$ 到 $16$。
• 教授不会经过绝对值大于 $100$ 的点。

大数据集（10 分，测试点 2 - 隐藏）

• $1 \leqslant L \leqslant 1000$
• 每个字符串 $S$ 的长度为 $1$ 到 $32$。
• 教授不会经过绝对值大于 $3000$ 的点。

由 ChatGPT 4.1 翻译