Description

国际象棋棋盘产业陷入了困境，需要你的帮助。鲜为人知的是，国际象棋棋盘是用极为稀有的克罗地亚棋盘树（Biggus Mobydiccus）的树皮制成的。这种树的树皮被剥下并展开成一个巨大的矩形棋盘材料。这个矩形是一个由黑白方格组成的网格。

你的任务是尽可能多地制作大型正方形棋盘。一个棋盘是树皮上的一个正方形区域，边与树皮矩形的边平行，且格子的颜色必须呈现棋盘的交错模式（即没有两个相同颜色的格子共边）。

每次你切割棋盘时，必须选择当前树皮上能切出的最大的棋盘。如果有多个同样大小的棋盘，选择最上面的那个。如果仍有多个，选择最左边的那个。不断切割，直到树皮上没有可以切出的棋盘为止。你可能需要切割出 $1 \times 1$ 的迷你棋盘。

下面是一个展示棋盘树树皮以及前几个被切割出的棋盘的例子。

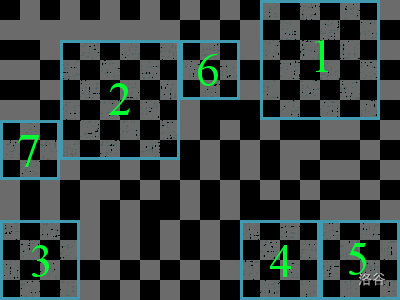
Input Format

输入的第一行是测试用例的数量 $T$。接下来有 $T$ 组测试数据。每组测试数据的第一行为树皮网格的尺寸 $M$ 和 $N$。$N$ 总是 $4$ 的倍数。接下来的 $M$ 行，每行包含一个长度为 $N/4$ 的十六进制整数，表示树皮网格的一行。将这些整数转为二进制后即可得到每一行的 $N$ 位，$0$ 表示黑格，$1$ 表示白格。输入中的行从上到下排列。在每一行中，十六进制整数的最高有效位对应该行最左侧的格子。

Output Format

对于每个测试用例，输出一行，格式为 “Case #$x$: $K$”，其中 $x$ 是测试用例编号（从 $1$ 开始），$K$ 是按照题目描述的切割过程可以切出的不同棋盘尺寸的数量。接下来的 $K$ 行，每行包含两个整数，分别表示棋盘的尺寸（从大到小排列）以及可以切出的该尺寸棋盘的数量。

4
15 20
55555
FFAAA
2AAD5
D552A
2AAD5
D542A
4AD4D
B52B2
52AAD
AD552
AA52D
AAAAA
5AA55
A55AA
5AA55
4 4
0
0
0
0
4 4
3
3
C
C
4 4
6
9
9
6

Case #1: 5
6 2
4 3
3 7
2 15
1 57
Case #2: 1
1 16
Case #3: 2
2 1
1 12
Case #4: 1
2 4

Hint

样例解释

第一个样例测试用例对应上图。

数据范围

• $1 \leq T \leq 100$；
• $N$ 一定是 $4$ 的倍数；
• 每个十六进制整数正好有 $N/4$ 个字符；
• 只会使用字符 $0$-$9$ 和 $A$-$F$。

小数据范围（18 分，测试点 1 - 可见）

• $1 \leq M \leq 32$；
• $1 \leq N \leq 32$。

大数据范围（24 分，测试点 2 - 隐藏）

• $1 \leq M \leq 512$；
• $1 \leq N \leq 512$；
• 输入文件大小不超过 200kB。

由 ChatGPT 4.1 翻译