Description

Yuki has a tree of size $n$.

Yuki defines the weight of a tree coloring scheme as follows:

Let $a$ be the sum of the squares of the sizes of all red maximal connected components.

Let $b$ be the sum of the squares of the sizes of all blue maximal connected components.

The weight of this coloring scheme is $ab$.

Some nodes on the tree have already been colored red or blue. Color the remaining nodes red or blue, and find the sum of the weights of all valid coloring schemes.

Let the number of nodes to be colored be $C$. Then there are $2^C$ valid coloring schemes in total.

The answer may be very large, so please modulo $998244353$.

Input Format

The first line inputs an integer $n$.

The next $n-1$ lines each contain two integers $u_i$ and $v_i$, representing an edge $(u_i, v_i)$ on the tree.

The next line contains a string $s$ of $n$ characters.

When $s_i=\texttt{r}$, the node is red.

When $s_i=\texttt{b}$, the node is blue.

When $s_i=\texttt{w}$, the node is to be colored.

Output Format

Output the answer modulo $998244353$.

6
1 2
1 3
1 4
2 5
2 6
rbwrbw

186

20
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 11
11 12
12 13
13 14
14 15
15 16
16 17
17 18
18 19
19 20
wwwwwwwwwwwwwwwwwwww

678428480

10
1 2
2 3
3 4
3 5
3 6
3 7
5 8
7 9
4 10
wbwwwrwrrw

8056

4
1 2
1 3
2 4
rbbr

4

5
1 2
1 3
2 4
3 5
wbwrw

100

7
1 2
1 3
2 4
2 5
3 6
3 7
wbwrwbr

294

Hint

Sample 1 explanation:

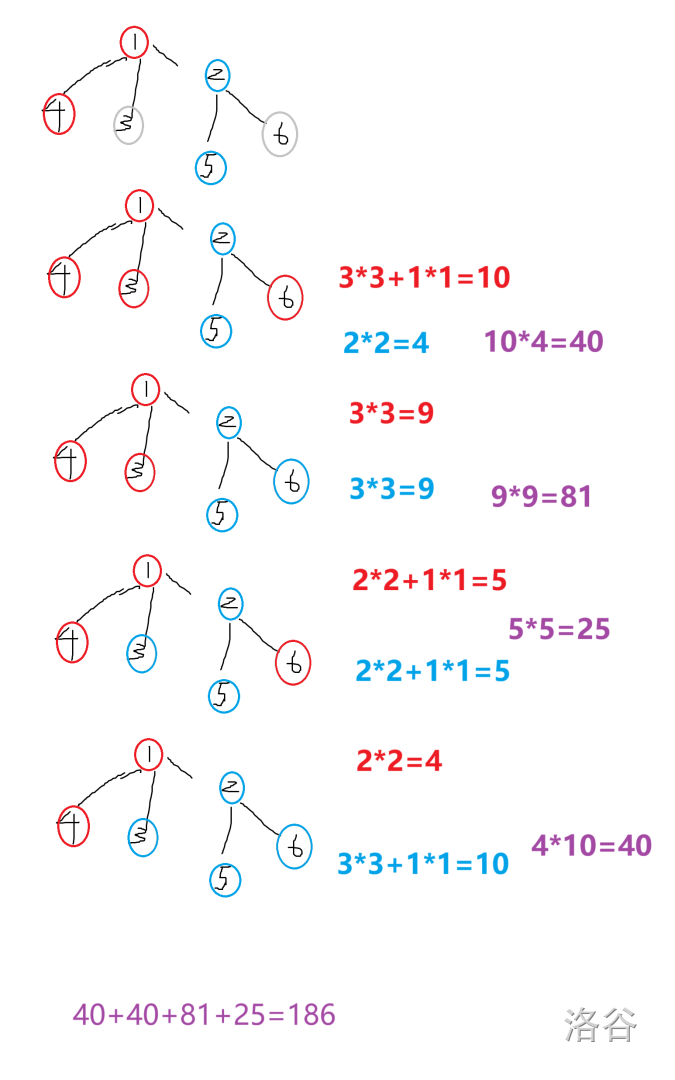
Test Case Distribution

For all data: $1\le n \le 2\times 10^6$, $s_i \in \{\texttt{r},\texttt{w},\texttt{b}\}$, $1\le u_i,v_i\le n$.