Description

我们将举办一场有 $2^N$ 支队伍参加的锦标赛，并为排名 $0$ 到 $P-1$ 的队伍颁发 $P$ 个完全相同的奖品。

所有队伍编号为 $0$ 到 $2^N-1$。当队伍 $i$ 与队伍 $j$ 进行比赛时，只有当 $i < j$ 时，队伍 $i$ 获胜。

锦标赛的队伍排列顺序称为锦标赛列表（tournament list），该列表包含了所有 $2^N$ 支参赛队伍。锦标赛列表会影响每轮比赛的对阵方式和顺序。

你的任务是：找出无论锦标赛列表如何排列，必定能获奖的最大编号队伍；以及存在某种锦标赛列表排列时，可能获奖的最大编号队伍。

锦标赛规则说明

锦标赛共进行 $N$ 轮。

每支队伍有一份战绩记录：即该队迄今为止每场比赛的胜负结果。例如，如果某支队伍打了三场，胜、负、胜，则其记录为 $[W, L, W]$。如果还未比赛，则记录为 $[]$。

每一轮，每支队伍都会与战绩记录相同的另一支队伍比赛。锦标赛列表中，拥有某一战绩的第一个队伍与第二个队伍对阵，第三个与第四个对阵，依此类推。

经过 $N$ 轮后，每支队伍都有独一无二的战绩。队伍排名按战绩的逆字典序排列：$[W, W, W] > [W, W, L] > [W, L, W] > [L, L, L]$。

以下是 $N=3$，锦标赛列表为 $[2, 4, 5, 3, 6, 7, 1, 0]$ 的一个示例。每一列表示不同的轮次，队伍按战绩分组。示例中获胜队伍已用 $*$ 标记。

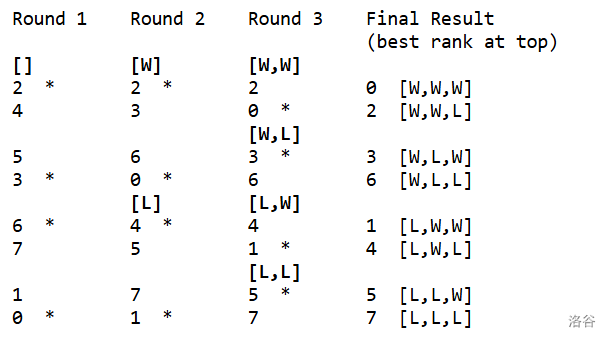
如果奖品数为 $4$（$N=3, P=4$），则奖品将发给队伍 $0$、$2$、$3$ 和 $6$。

对于 $N=3, P=4$，无论锦标赛列表如何排列，必定能获奖的最大编号队伍为 $0$：本锦标赛列表说明队伍 $1$ 可能无法获奖，而队伍 $0$ 无论如何总能获奖。

对于 $N=3, P=4$，存在某种锦标赛列表排列时，可能获奖的最大编号队伍为 $6$：本锦标赛列表说明队伍 $6$ 可能获奖，而队伍 $7$ 无论如何都无法获奖。

Input Format

输入的第一行为测试用例数 $T$。接下来 $T$ 个测试用例，每个用两整数 $N$ 和 $P$ 表示，含义如上。

Output Format

对于每个测试用例，输出一行 "Case #x: y z"，其中 $x$ 为测试用例编号（从 $1$ 开始），$y$ 表示无论锦标赛列表如何排列，必定能获奖的最大编号队伍，$z$ 表示存在某种锦标赛列表排列时，可能获奖的最大编号队伍。

3
3 4
3 5
3 3

Case #1: 0 6
Case #2: 2 6
Case #3: 0 4

Hint

限制条件

• $1 \leq T \leq 100$
• $1 \leq P \leq 2^N$

小数据集（7 分，测试集 1 - 可见）

• $1 \leq N \leq 10$

大数据集（13 分，测试集 2 - 隐藏）

• $1 \leq N \leq 50$

翻译由 ChatGPT-4.1 完成。