Description

本题中，你的任务是在一个 $N \times M$ 的矩形网格上放置尽可能少的石头，以便围住至少 $K$ 个交叉点。这个网格由 $N$ 条水平线段和 $M$ 条垂直线段组成，它们的交点构成了交叉点。

某个交叉点被认为是“被围住”的，当且仅当以下两种情况之一成立：

1. 在该点上放置了一个石头；
2. 从该点出发，无法仅沿网格线，经过空交叉点，到达网格边缘上的空交叉点。

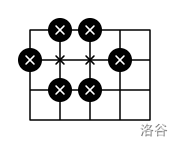
例如，要在一个 $4 \times 5$ 的网格中围住 $8$ 个交叉点，至少需要放置 $6$ 个石头。下面展示了一个合法的石头放置方案。被围住的交叉点用 "x" 标记。

Input Format

输入的第一行是测试用例的数量 $T$。接下来的 $T$ 行，每行包含三个整数：$N$、$M$ 和 $K$，分别表示网格的行数、列数以及需要被围住的交叉点数量。

Output Format

对于每个测试用例，输出一行，格式为 "Case #x: y"，其中 $x$ 是测试用例编号（从 1 开始），$y$ 是围住至少 $K$ 个交叉点所需的最少石头数。

2
4 5 8
3 5 11

Case #1: 6
Case #2: 8

Hint

样例说明

• 在第一个样例中，需要在 $4 \times 5$ 的网格中围住至少 $8$ 个交叉点，最少需要放置 $6$ 个石头。
• 在第二个样例中，要围住 $11$ 个交叉点，最少需要放置 $8$ 个石头。

限制条件

• $1 \leq T \leq 100$
• $1 \leq N$
• $1 \leq M$
• $1 \leq K \leq N \times M$

Small 数据集（15 分）

• 时间限制：60 3 秒。
• $N \times M \leq 20$

Large 数据集（30 分）

• 时间限制：120 10 秒。
• $N \times M \leq 1000$

翻译由 ChatGPT-4o 完成