Description

你是歌剧中的一个小角色——塞维利亚的园丁。歌剧的舞台背景是一个由单位格组成的矩形庭院，共有 $\mathbf{R}$ 行 $\mathbf{C}$ 列。你被要求在庭院中布置一组树篱迷宫：每个格子都必须放置一根对角树篱。对于任意一个格子，有两种可能的树篱类型：从左下到右上（用 / 表示），或从左上到右下（用 \ 表示）。任何相邻的树篱相接处都会形成一堵连续的墙。

庭院外围有一圈单位格，宽度为一格，四个角格子缺失。每一个外围格子里都住着一位廷臣。外围格子的编号顺时针排列，从顶行最左侧的格子编号为 1，最后一个编号为 $2 \times (\mathbf{R}+\mathbf{C})$，即左列最顶端的格子。例如，当 $\mathbf{R}=2, \mathbf{C}=2$ 时，外围格子的编号如下（注意，此时还未放置树篱）：

 12 
8  3
7  4
 65

在这个与众不同的歌剧中，爱情是互相且唯一的：每位廷臣只爱一位其他廷臣，且这份爱是双向且专属的。每位廷臣都希望能穿越树篱迷宫，悄悄地与心上人相会，并且不被其他廷臣遇见。也就是说，任意一对恋人廷臣之间，必须存在一条只属于他们两人的、被树篱墙与其他路径完全隔开的通路。迷宫中可以存在不属于任何廷臣路径的部分，只要所有恋人对都能连通即可。

给定所有恋人配对关系，你能否构造出这样一组树篱迷宫，使得每一对恋人都能连通？如无法实现，请输出 IMPOSSIBLE。

Input Format

输入的第一行包含一个整数 $\mathbf{T}$，表示测试用例组数。接下来有 $\mathbf{T}$ 组测试用例，每组包含两行。第一行为两个整数 $\mathbf{R}$ 和 $\mathbf{C}$，表示庭院的行数和列数。第二行为一个长度为 $2 \times (\mathbf{R}+\mathbf{C})$ 的排列，包含所有廷臣的编号。第 1、2 个编号为一对恋人，第 3、4 个编号为一对恋人，以此类推。

Output Format

对于每组测试用例，先输出一行 Case #x:，其中 $x$ 为测试用例编号（从 1 开始）。如果无法满足条件，再输出一行 IMPOSSIBLE。否则，输出 $\mathbf{R}$ 行，每行 $\mathbf{C}$ 个字符，表示一个合法的树篱迷宫，每个字符为 / 或 \。迷宫中的每个格子都必须填满，不能留空。若存在多种方案，你可任选其一输出。

4
1 1
1 4 3 2
1 3
1 8 2 7 3 4 5 6
2 2
8 1 4 5 2 3 7 6
1 1
1 3 2 4

Case #1:
/
Case #2:
//\
Case #3:
//
\/
Case #4:
IMPOSSIBLE

Hint

样例解释

在第 3 组中，恋人配对为 $(8, 1), (4, 5), (2, 3), (7, 6)$。如下是样例输出的示意图：

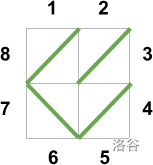
对于第 3 组，下面这种迷宫也是合法的：

/\
\/

在第 4 组中，庭院仅有一个格子，外围廷臣编号按顺时针分别为 1、2、3、4。此时只有两种放置方式：/ 或 \。第一种会形成 1 到 4、2 到 3 的通路，第二种会形成 1 到 2、3 到 4 的通路。但本组数据中 1 爱 3、2 爱 4，无论哪种方式都无法满足条件，因此输出 IMPOSSIBLE，歌剧中将充满悲伤的咏叹调！

限制条件

小数据集（6 分，测试集 1 - 可见）

• $1 \leqslant \mathbf{T} \leqslant 100$。
• $1 \leqslant \mathbf{R} \times \mathbf{C} \leqslant 16$。

大数据集（23 分，测试集 2 - 隐藏）

• $1 \leqslant \mathbf{T} \leqslant 500$。
• $1 \leqslant \mathbf{R} \times \mathbf{C} \leqslant 100$。

翻译由 GPT4.1 完成。