Description

你被要求组织一场石头-剪刀-布锦标赛。该锦标赛采用单败淘汰制，将进行 $\mathrm{N}$ 轮比赛；共有 $2^{\mathrm{N}}$ 名选手参赛。

最初，选手们将按照你指定的顺序从左到右排成一列。在每一轮中，队列中第 1 和第 2 名选手（从左到右）进行一场对决，第 3 和第 4 名选手（如果存在）也进行对决，以此类推；所有这些对决将同时进行。每场对决的胜者将留在队列中，保持相对顺序不变，败者则离开队列回家。随后开始新一轮比赛。如此反复，直到队列中只剩一名选手；该选手即为冠军。

在每场石头-剪刀-布对决中，双方选手各自秘密选择石头（Rock）、布（Paper）或剪刀（Scissors）中的一种，然后比较选择。石头胜剪刀，剪刀胜布，布胜石头。如果一方的选择能击败对方，则该方获胜，对决结束。然而，如果双方选择相同，则为平局，他们必须重新选择并继续比，直到分出胜负为止。

你知道，今年的选手们都很固执且毫无策略性。每位选手都有自己偏好的手势，并且无论对手如何，每场比赛都只会出这个手势。因此，如果两位出同样手势的选手对决，他们会一直打平，这场比赛永远不会结束！如果出现这种情况，整个锦标赛将无法结束，你也会沦为笑柄。

今年，有 $\mathbf{R}$ 名选手只出石头（Rock），$\mathbf{P}$ 名选手只出布（Paper），$\mathbf{S}$ 名选手只出剪刀（Scissors）。鉴于此，你希望安排一个选手顺序，保证锦标赛一定可以顺利进行并决出唯一冠军——即任何一场比赛都不会出现平局。你的老板要求你列出所有满足条件的初始排列（按从左到右顺序，用 $\mathrm{R}$、$\mathrm{P}$、$\mathrm{S}$ 分别代表偏好石头、布、剪刀的选手），然后按字典序排序。

你知道老板会懒得看完整个列表，只会挑第一个排列；你能告诉老板这个排列是什么吗？还是你必须告诉老板无法避免平局（即 IMPOSSIBLE）？

Input Format

输入的第一行包含一个整数 $\mathbf{T}$，表示测试用例数量。接下来有 $\mathbf{T}$ 行，每行对应一个测试用例。每个测试用例包含四个整数：$\mathbf{N}, \mathbf{R}, \mathbf{P}, \mathbf{S}$，含义如上所述。

Output Format

对于每组测试用例，输出一行 Case #x: y，其中 $\mathrm{x}$ 表示测试用例编号（从 1 开始），$\mathrm{y}$ 要么是 IMPOSSIBLE，要么是一个长度为 $2^{\mathrm{N}}$ 的字符串，表示字典序最小的、满足要求的初始选手排列。排列中的每个字符必须是 $\mathrm{R}$、$\mathrm{P}$ 或 $\mathrm{S}$，并且总共有 $\mathbf{R}$ 个 R，$\mathbf{P}$ 个 P，$\mathbf{S}$ 个 S。

4
1 1 1 0
1 2 0 0
2 1 1 2
2 2 0 2

Case #1: PR
Case #2: IMPOSSIBLE
Case #3: PSRS
Case #4: IMPOSSIBLE

Hint

样例解释

在样例第 1 组中，只有两名选手，比赛只进行一轮。无论两人顺序如何，布选手都会击败石头选手。你将向老板提供按字典序排序的 PR、RP，首个排列为 PR。

在样例第 2 组中，两名选手都只出石头，无法避免平局。

在样例第 3 组中，共有四名选手，比赛进行两轮。第一轮，第一名（布）输给第二名（剪刀），第三名（石头）击败第四名（剪刀）。第二轮，队列变为 SR，第一名（剪刀）输给第二名（石头），比赛顺利结束且无平局。

以下是样例第 3 组的比赛流程示意图：

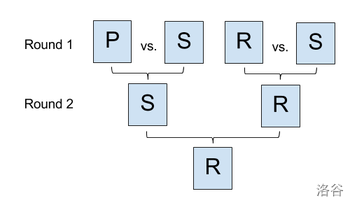
其他排列如 PSSR 也会出现在你给老板的列表中，但 PSRS 是字典序最小的。

在样例第 4 组中，唯一能安排首轮无平局的方式是让两场比赛分别为一名石头对一名剪刀。但这样会有两名石头选手晋级，下一轮他们会相遇并陷入平局。

限制条件

• $\mathbf{R}+\mathbf{P}+\mathbf{S}=2^{\mathbf{N}}$。
• $0 \leqslant \mathbf{R} \leqslant 2^{\mathbf{N}}$。
• $0 \leqslant \mathbf{P} \leqslant 2^{\mathbf{N}}$。
• $0 \leqslant \mathbf{S} \leqslant 2^{\mathbf{N}}$。

小数据集（4 分，测试集 1 - 可见）

• $1 \leqslant \mathbf{T} \leqslant 25$。
• $1 \leqslant \mathbf{N} \leqslant 3$。

大数据集（14 分，测试集 2 - 隐藏）

• $1 \leqslant \mathbf{T} \leqslant 75$。
• $1 \leqslant \mathbf{N} \leqslant 12$。

翻译由 GPT4.1 完成。