Description

你是一名“Fence Construction Company”（围栏建造公司）的员工，被分配去建造 $F$ 段围栏。每段围栏都是一条从一个点到另一个点的直线段。形式化地说，每段围栏是连接二维平面上两个不同点的线段。围栏之间不会相互相交，除了可能在端点处。所有围栏是连通的，即对于任意两段围栏 $f$ 和 $g$，都存在一条路径 $f = f_1, f_2, \dots, f_k = g$，使得 $f_i$ 与 $f_{i+1}$ 共享一个端点。

在你开始工作时，尚未建造任何围栏。建造工作通过一种特殊的“围栏发射”3D 打印机完成。只有一台这样的设备，因此围栏需要一段一段地建造。打印机足够小，可以视为平面上的一个点。

要建造某段围栏 $f$，你必须首先将打印机放置在平面上的某个点 $p$，使得打印机能够“看到”整个 $f$，且视线不会被之前建造的围栏阻挡。形式化地说，$p$ 必须满足：

• $p$ 不能在 $f$ 上（包括端点）。
• 对于 $f$ 上的任意非端点 $q$，连接 $p$ 和 $q$ 的线段不能与任何已建造的围栏相交。

移动打印机时，你可以从当前位置沿着一条连续但不一定直的路径移动，只要这条路径不与任何已建造的围栏相交（包括端点）。在建造第一段围栏之前和最后一段围栏之后，你可以选择打印机的任意位置。

由于需要遵循上述流程，你并不总能以任意顺序建造围栏。例如，你可能选择了一个顺序，结果把打印机困在某处，无法移动到需要的位置。

公司主管已经为 $K$ 段围栏指定了一个相对顺序（但这些围栏都还未建造），但他并未深思熟虑。为了避免惹怒主管，你需要遵循这个顺序，并将剩下的 $F-K$ 段围栏插入到任意位置以完成整个顺序。

在这些限制下，请找出一种建造围栏的顺序。保证至少存在一种合法的顺序。

Input Format

输入的第一行为测试用例数 $T$。接下来有 $T$ 组测试数据。每组测试数据的第一行为两个整数 $F$ 和 $K$，分别表示围栏总数和主管指定顺序中的围栏数。接下来 $F$ 行，第 $i$ 行（从 1 开始计数）包含四个整数 $A_i$、$B_i$、$C_i$ 和 $D_i$，表示第 $i$ 段围栏是从点 $(A_i, B_i)$ 到 $(C_i, D_i)$ 的线段。输入中的前 $K$ 段围栏即为主管指定顺序中的围栏。

Output Format

对于每组测试数据，输出一行，格式为 Case #x: y，其中 $x$ 为测试用例编号（从 1 开始），$y$ 为一个用空格分隔的 $1$ 到 $F$ 的整数排列，表示一种合法的建造围栏顺序。

3
6 2
0 0 7 7
15 -2 10 0
0 0 0 10
0 0 10 0
0 10 10 10
10 0 10 10
6 1
0 0 0 10
0 0 10 0
0 10 10 10
10 0 10 10
0 0 7 7
15 -2 10 0
11 4
-10 0 10 0
-10 0 0 10
10 0 0 10
0 2 0 5
0 2 10 0
10 0 0 5
15 3 18 3
15 3 15 9
18 3 15 9
15 3 16 5
0 10 15 3

Case #1: 1 2 3 4 5 6
Case #2: 5 6 1 2 3 4
Case #3: 11 10 7 8 9 1 2 3 6 5 4

Hint

样例解释

注意，最后一个样例不会出现在测试集 1 中。

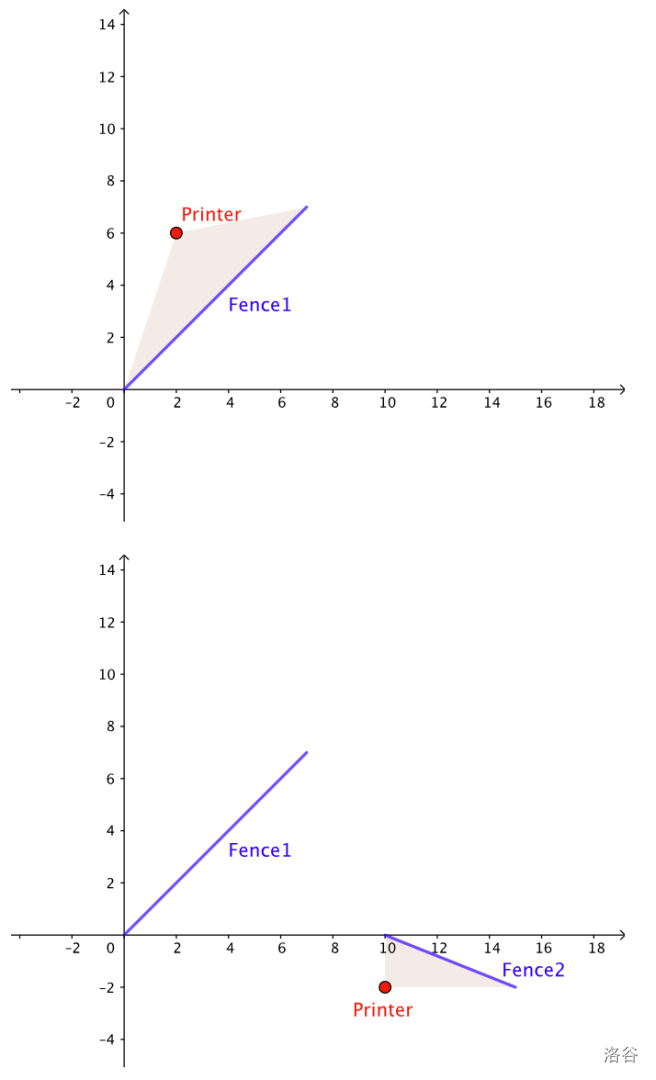
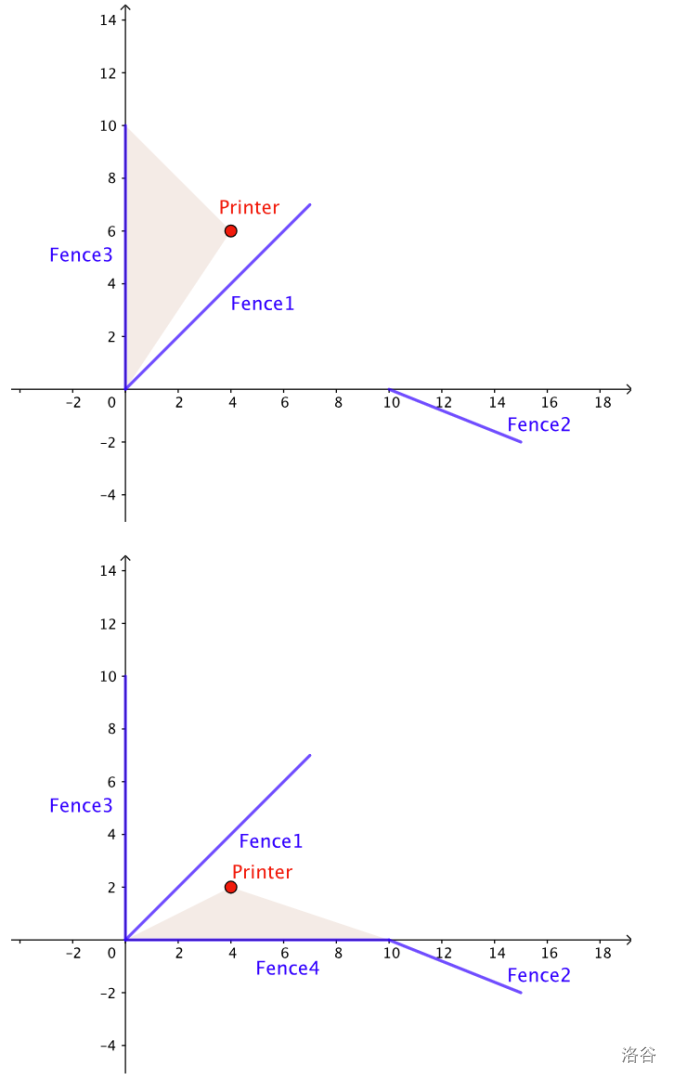
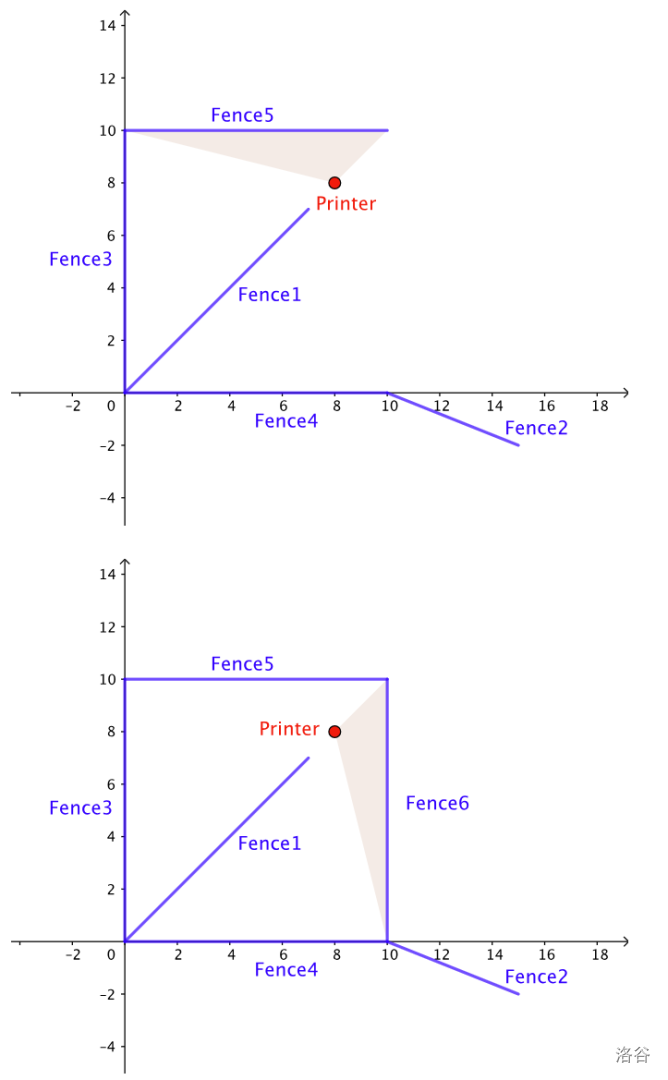
在样例 1 中，可以按给定顺序建造围栏：$1, 2, 3, 4, 5, 6$。注意，围栏 $1$ 必须在围栏 $2$ 之前建造，这是主管的要求。

在样例 2 中，无法按给定顺序建造围栏！一种可行的顺序是：$5, 6, 1, 2, 3, 4$。注意，当主管指定的顺序只包含一段围栏时，相对顺序条件总是自动满足。

在样例 3 中，可以按顺序建造：$11, 10, 7, 8, 9, 1, 2, 3, 6, 5, 4$。注意，围栏 $1, 2, 3, 4$ 必须按这个相对顺序建造。

下图展示了样例 1 的一种合法建造方式。

数据范围

• $1 \leq T \leq 100$。
• $4 \leq F \leq 300$。
• $-10^5 \leq A_i \leq 10^5$，对所有 $i$。
• $-10^5 \leq B_i \leq 10^5$，对所有 $i$。
• $-10^5 \leq C_i \leq 10^5$，对所有 $i$。
• $-10^5 \leq D_i \leq 10^5$，对所有 $i$。
• $(A_i, B_i) \neq (C_i, D_i)$，对所有 $i$。
• 如果 $p$ 是某段围栏上的非端点，则 $p$ 不是任何其他围栏上的点。
• 给定的围栏是连通的，如题目描述所定义。
• 至少存在一种满足所有建造限制的围栏顺序。

测试集 1（12 分，公开）

• $1 \leq K \leq 2$。

测试集 2（23 分，隐藏）

• $1 \leq K < F$。

由 ChatGPT 4.1 翻译