Description

一艘神秘的立方体外星飞船出现在多伦多上空！在本题中，多伦多被视为三维空间中一条平行于 $xz$ 平面的平面，位于 $y = -3$ 千米处。外星飞船是一个边长为 $1$ 千米的实心立方体，中心在 $(0\,\text{km}, 0\,\text{km}, 0\,\text{km})$，其八个顶点分别为 $(\pm 0.5\,\text{km}, \pm 0.5\,\text{km}, \pm 0.5\,\text{km})$。飞船在该平面上投下了一个不祥的影子；形式上，这个影子是立方体在该平面上的正交投影（我们认为太阳是一个位于 $y$ 轴正方向无限远处的点光源）。

军方表示，只要外星人满足他们的官僚要求：影子在平面上覆盖的面积必须与 $\mathbf{A}\,\text{km}^2$ 足够接近（具体定义见输出部分），他们就可以容忍飞船的存在。他们雇佣了你——一位几何语言学专家——来向外星人传达这一要求。你已经了解到，飞船不能改变大小，中心也不能移动，但可以在原地任意旋转。

请你找出一种旋转方式，使得飞船的影子面积接近 $\mathbf{A}$。你需要用三个点来表达旋转方式：任选三个互不相对的面心。

Input Format

第一行输入一个整数 $\mathbf{T}$，表示测试用例的数量。接下来有 $\mathbf{T}$ 组测试数据，每组一行，包含一个有理数 $\mathbf{A}$，表示期望的影子面积（单位为 $\mathrm{km}^2$），精确到小数点后六位。

保证对于本题允许的 $\mathbf{A}$ 取值，总存在一种旋转方式使得飞船满足要求。

Output Format

对于每个测试用例，首先输出一行 Case #x:，其中 $x$ 是测试用例编号（从 1 开始）。然后输出三行，每行三个有理数，分别为你选择的三个面心的 $x, y, z$ 坐标。你可以使用十进制（如 0.000123456）或科学计数法（如 1.23456e-4）输出。

你的答案仅当同时满足以下所有条件时才被认为是正确的：

1. 每个点到原点的距离必须在 $0.5-10^{-6}$ 到 $0.5+10^{-6}$ 千米之间（含端点）。
2. 连接原点到每个点的线段，两两夹角（弧度）必须在 $\pi/2-10^{-6}$ 到 $\pi/2+10^{-6}$ 之间（含端点）。
3. 影子的面积（单位为 $\mathrm{km}^2$），通过将所有 8 个顶点投影到 $y=-3$ 平面并计算这些投影点的凸包面积得到，必须在 $\mathbf{A}-10^{-6}$ 到 $\mathbf{A}+10^{-6}$ 之间（含端点）。我们将顶点计算为 $+/-\mathbf{p}_1+/-\mathbf{p}_2+/-\mathbf{p}_3$（即对于每个 $\mathbf{p}_i$，取 $+\mathbf{p}_i$ 或 $-\mathbf{p}_i$，向量相加），其中 $\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3$ 是你提供的三个面心。

请注意，你可能需要输出超过 6 位小数以通过上述判定。如果存在多个可行解，你可以输出任意一个。

2
1.000000
1.414213

Case #1:
0.5 0 0
0 0.5 0
0 0 0.5
Case #2:
0.3535533905932738 0.3535533905932738 0
-0.3535533905932738 0.3535533905932738 0
0 0 0.5

Hint

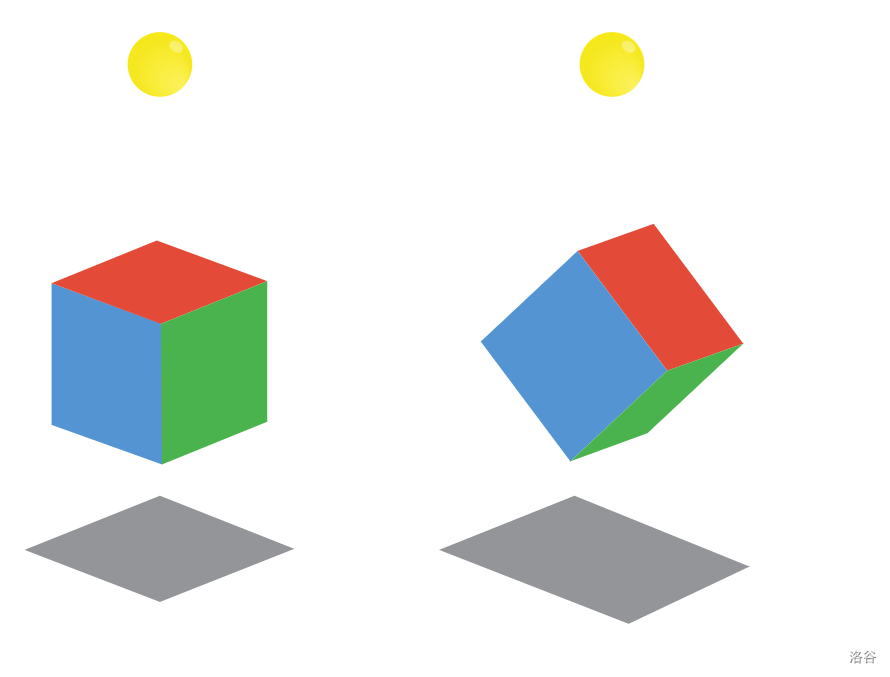
在样例 1 中，立方体无需旋转；此时有两个面已经与平面平行，影子是边长为 $1$ 的正方形。

在样例 2 中，一种可行解是让立方体绕 $x=y=0$ 这条线旋转 $45$ 度，此时影子是 $1$ 和 $\sqrt{2}$ 的矩形。

下图为样例 1 和样例 2 的立方体及其影子示意图。太阳仅为说明而画出，实际应视为位于 $y$ 轴正方向无限远处的点。

数据范围

• $1 \leqslant \mathrm{T} \leqslant 100$。

测试点 1（可见）

• $1.000000 \leqslant \mathrm{A} \leqslant 1.414213$

测试点 2（隐藏）

• $1.000000 \leqslant \mathrm{A} \leqslant 1.732050$

由 ChatGPT 4.1 翻译